Exercicios de Matematica 12 ANO - Teorema de Bolzano - Exercício 1
Considere, para um certo número real  positivo, uma função
positivo, uma função  , contínua, de domínio
, contínua, de domínio ![\left[ { - a,a} \right] \left[ { - a,a} \right]](/images/jlatex/8f7789c40e13a9d56fc3916d7d539b99.gif) .
.
Sabe-se que 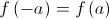 e
e 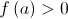 .
.
Mostre que a condição 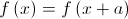 tem, pelo menos, uma solução em
tem, pelo menos, uma solução em ![\left] { - a,0} \right[ \left] { - a,0} \right[](/images/jlatex/c6c78f699a4b8bc661c121630153e0b9.gif) .
.
Considere, para um certo número real  positivo, uma função
positivo, uma função  , contínua, de domínio
, contínua, de domínio ![\left[ { - a,a} \right] \left[ { - a,a} \right]](/images/jlatex/8f7789c40e13a9d56fc3916d7d539b99.gif) .
.
Sabe-se que 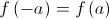 e
e 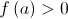 .
.
Mostre que a condição 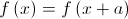 tem, pelo menos, uma solução em
tem, pelo menos, uma solução em ![\left] { - a,0} \right[ \left] { - a,0} \right[](/images/jlatex/c6c78f699a4b8bc661c121630153e0b9.gif) .
.
4. Seja  uma função de domínio
uma função de domínio  , definida por
, definida por 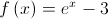 .
.
Em qual dos intervalos seguintes o teorema de Bolzano permite afirmar que a equação 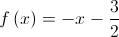 tem, pelo menos, uma solução?
tem, pelo menos, uma solução?
(A) ![\left] {0,\frac{1}{5}} \right[ \left] {0,\frac{1}{5}} \right[](/images/jlatex/8e6ce860f903710a57906abcb2e93ee7.gif)
(B) ![\left] {\frac{1}{5},\frac{1}{4}} \right[ \left] {\frac{1}{5},\frac{1}{4}} \right[](/images/jlatex/5d89a8c399c9af7d86f6f1612d1a8e48.gif)
(C) ![\left] {\frac{1}{4},\frac{1}{3}} \right[ \left] {\frac{1}{4},\frac{1}{3}} \right[](/images/jlatex/7ec4e81ebb60f3ecb9988283a0caf3f7.gif)
(D) ![\left] {\frac{1}{3},1} \right[ \left] {\frac{1}{3},1} \right[](/images/jlatex/dfcb0c63fea9a7c21465e157b1264946.gif)
Seja  uma função de domínio
uma função de domínio 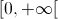 , definida por:
, definida por:
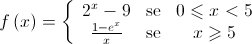
Em qual dos intervalos seguintes o teorema de Bolzano permite garantir a existência de, pelo menos, um zero da função  ?
?
(A) ![\left] {0,1} \right[ \left] {0,1} \right[](/images/jlatex/3f310af7ae64b30edb352537f24808b4.gif)
(B) ![\left] {1,4} \right[ \left] {1,4} \right[](/images/jlatex/f2e09f26592828145a7fb3609035a8b0.gif)
(C) ![\left] {4,6} \right[ \left] {4,6} \right[](/images/jlatex/ced08cb5c2687456b084c0ae272cc71f.gif)
(D) ![\left] {6,7} \right[ \left] {6,7} \right[](/images/jlatex/b438c177bea9775a37494f059c2f6554.gif)
Exame Nacional de Matemática 12º Ano 1ª Fase 2011 - Grupo 1 - Exercício 4→
Considere, para um certo número real 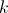 , a função
, a função  , de domínio
, de domínio  , definida por
, definida por 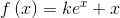 .
.
O teorema de Bolzano garante que a função  tem, pelo menos, um zero no intervalo
tem, pelo menos, um zero no intervalo ![\left] {0,1} \right[ \left] {0,1} \right[](/images/jlatex/3f310af7ae64b30edb352537f24808b4.gif) .
.
A qual dos intervalos seguintes pode pertencer 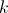 ?
?
(A) ![\left] { - e, - \frac{1}{e}} \right[ \left] { - e, - \frac{1}{e}} \right[](/images/jlatex/01e51dde1da510e6847872057c1737b8.gif)
(B) ![\left] { - \frac{1}{e},0} \right[ \left] { - \frac{1}{e},0} \right[](/images/jlatex/4e83ddf76c73db6816f1d482a9cd5a81.gif)
(C) ![\left] {0,\frac{1}{e}} \right[ \left] {0,\frac{1}{e}} \right[](/images/jlatex/a8e277bcc97066f8a808733b05534d04.gif)
(D) ![\left] {\frac{1}{e},1} \right[ \left] {\frac{1}{e},1} \right[](/images/jlatex/688febe6f43feddd9f13368603febef4.gif)
Exame Nacional de Matemática 12º Ano 1ª Fase 2014 - Grupo 1 - Exercício 4→