Atividades Educativas

Atividades Para Imprimir

Exercícios de Matemática

Jogos de Matematica

Exames de Matemática

Exames de Matemática A12º ANO

Exames de Matemática B10º ANO e 11º ANO

Exame Nacional de Matemática 12º Ano 1ª Fase 2012 - Grupo 1 - Exercício 4

4. Seja uma função de domínio $\mathbb{R}$ , definida por 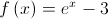$f\left( x \right) = {e^x} - 3$ .

Em qual dos intervalos seguintes o teorema de Bolzano permite afirmar que a equação 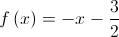$f\left( x \right) = - x - \frac{3}{2}$ tem, pelo menos, uma solução?

(A) $\left] {0,\frac{1}{5}} \right[$

(B) $\left] {\frac{1}{5},\frac{1}{4}} \right[$

(C) $\left] {\frac{1}{4},\frac{1}{3}} \right[$

(D) $\left] {\frac{1}{3},1} \right[$

Resolução do exercício de matemática:

Solução: (B)

$f\left( x \right) = - x - \frac{3}{2} \Leftrightarrow {e^x} - 3 = - x - \frac{3}{2} \Leftrightarrow {e^x} - 3 + x + \frac{3}{2} = 0 \Leftrightarrow {e^x} + x - \frac{3}{2} = 0$

Seja $g\left( x \right) = {e^x} + x - \frac{3}{2}$ .

é contínua em $\mathbb{R}$ , logo é contínua em qualquer os intervalos correspondentes às opções.

Como:

$g\left( 0 \right) < 0$ ; $g\left( {\frac{1}{5}} \right) < 0$ ; $g\left( {\frac{1}{4}} \right) > 0$ ; $g\left( {\frac{1}{3}} \right) > 0$ ; $g\left( 1 \right) > 0$

Logo, $g\left( {\frac{1}{5}} \right) \times g\left( {\frac{1}{4}} \right) < 0$ .

Logo, a função tem pelo menos um zero no intervalo $\left] {\frac{1}{5},\frac{1}{4}} \right[$ .

Atividades Relacionadas

Tabuadas Para Imprimir e Colorir

Tabuadas do Ben 10 Para Colorir

Tabuadas do Sonic Para Colorir

Tabuadas da Hello Kitty Para Colorir

Tabuadas do Batman Para Colorir

Tabuadas do Homem Aranha Para Colorir