Exame Nacional de Matemática 12º Ano 2ª Fase 2011 - Grupo 2 - Exercício 6
Para , números reais positivos, considere a função
, números reais positivos, considere a função , de domínio
, de domínio , definida por:
, definida por:

Seja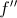 a segunda derivada da função
a segunda derivada da função .
.
Mostre que , para qualquer número real
, para qualquer número real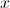 .
.

Para , números reais positivos, considere a função
, números reais positivos, considere a função , de domínio
, de domínio , definida por:
, definida por:

Seja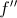 a segunda derivada da função
a segunda derivada da função .
.
Mostre que , para qualquer número real
, para qualquer número real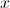 .
.
Considere a função 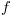 , de domínio
, de domínio 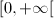 , definida por
, definida por
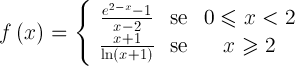
Resolva os três itens seguintes recorrendo a métodos exclusivamente analíticos.
1.
Estude  quanto à existência de assíntotas verticais do seu gráfico.
quanto à existência de assíntotas verticais do seu gráfico.
2.
Mostre, sem resolver a equação, que 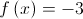 tem, pelo menos, uma solução em
tem, pelo menos, uma solução em ![\left] {0,\frac{1}{2}} \right[ \left] {0,\frac{1}{2}} \right[](/images/jlatex/3a22da03bfe5e59c313c4ed2e8900ff7.gif) .
.
3.
Estude  quanto à monotonia em
quanto à monotonia em ![\left] {2, + \infty } \right[ \left] {2, + \infty } \right[](/images/jlatex/aba2e90d9254a962a10b0d0dbae4eefa.gif) .
.
Exame Nacional de Matemática 12º Ano 2ª Fase 2011 - Grupo 2 - Exercício 5→
Considere a função  , de domínio
, de domínio ![\left] {0,\frac{\pi }{2}} \right[ \left] {0,\frac{\pi }{2}} \right[](/images/jlatex/a3ff389e6a2249f282d58eca9edd8dbe.gif) , definida por
, definida por

Sabe-se que:
•  é um ponto do gráfico de
é um ponto do gráfico de
• a reta de equação  é paralela à reta tangente ao gráfico
é paralela à reta tangente ao gráfico de no ponto
de no ponto
Determine, recorrendo à calculadora gráfica, a abcissa do ponto .
.
Na sua resposta, deve:
• equacionar o problema;
• reproduzir o gráfico da função ou os gráficos das funções que tiver necessidade de visualizar na calculadora, devidamente identificado(s), incluindo o referencial;
• indicar a abcissa do ponto  com arredondamento às centésimas.
com arredondamento às centésimas.
Exame Nacional de Matemática 12º Ano 2ª Fase 2011 - Grupo 2 - Exercício 4→
Na estufa de um certo jardim botânico, existem dois lagos aquecidos, o lago e o lago
e o lago .
.
Às zero horas do dia 1 de março de 2010, cada lago recebeu uma espécie diferente de nenúfares, a saber, Victoria amazonica e Victoria cruziana.
 é o número aproximado de nenúfares existentes no lago
é o número aproximado de nenúfares existentes no lago ,
,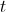 dias após as zero horas do dia 1 de março de 2010. Esses nenúfares são da espécie Victoria amazonica e desenvolvem-se segundo o modelo:
dias após as zero horas do dia 1 de março de 2010. Esses nenúfares são da espécie Victoria amazonica e desenvolvem-se segundo o modelo:
 , com
, com
 é o número aproximado de nenúfares existentes no lago
é o número aproximado de nenúfares existentes no lago ,
, 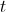 dias após as zero horas do dia 1 de março de 2010. Esses nenúfares são da espécie Victoria cruziana e desenvolvem-se segundo o modelo
dias após as zero horas do dia 1 de março de 2010. Esses nenúfares são da espécie Victoria cruziana e desenvolvem-se segundo o modelo
 , com
, com
Resolva os dois itens seguintes recorrendo a métodos exclusivamente analíticos.
1.
Como foi referido, às zero horas do dia 1 de março de 2010, o lago recebeu um certo número de nenúfares da espécie Victoria amazonica. Decorridos 7 dias, esse número aumentou.
recebeu um certo número de nenúfares da espécie Victoria amazonica. Decorridos 7 dias, esse número aumentou.
Determine de quanto foi esse aumento.
Apresente o resultado com arredondamento às unidades.
2.
Determine quantos dias foram necessários, após as zero horas do dia 1 de março de 2010, para que o número de nenúfares existentes no lago fosse igual ao número de nenúfares existentes no lago
fosse igual ao número de nenúfares existentes no lago  .
.
Apresente o resultado com arredondamento às unidades.
Exame Nacional de Matemática 12º Ano 2ª Fase 2011 - Grupo 2 - Exercício 3→A MatFinance é uma empresa de consultoria financeira.
1.
Dos funcionários da MatFinance, sabe-se que:
Determine a probabilidade de um desses funcionários, escolhido ao acaso, ser licenciado, sabendo que tem idade não inferior a 40 anos.
Apresente o resultado na forma de fração irredutível.
2.
Considere o problema seguinte.
«Foi pedido a 15 funcionários da MatFinance que se pronunciassem sobre um novo horário de trabalho.
Desses 15 funcionários, 9 estão a favor do novo horário, 4 estão contra, e os restantes estão indecisos.
Escolhe-se, ao acaso, 3 funcionários de entre os 15 funcionários considerados.
De quantas maneiras diferentes podem ser escolhidos os 3 funcionários, de forma que pelo menos 2 dos funcionários escolhidos estejam a favor do novo horário de trabalho?»
Apresentam-se, em seguida, duas respostas.
Resposta I: Resposta II:
Resposta II: 
Apenas uma das respostas está correta.
Elabore uma composição na qual:
explique, no contexto do problema, a razão da alteração proposta.
Exame Nacional de Matemática 12º Ano 2ª Fase 2011 - Grupo 2 - Exercício 2→Seja 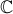 o conjunto dos números complexos.
o conjunto dos números complexos.
Resolva os dois itens seguintes sem recorrer à calculadora.
1.
Considere e
e  , com
, com  e
e  .
.
Determine o valor de para o qual
para o qual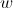 é um número real.
é um número real.
2.
Seja  um número complexo tal que
um número complexo tal que  .
.
Mostre que  .
.
Exame Nacional de Matemática 12º Ano 2ª Fase 2011 - Grupo 2 - Exercício 1→
Na Figura 4, estão representadas, no plano complexo, as imagens geométricas de
seis números complexos 

Qual é o número complexo que pode ser igual a  ?
?
(A) 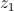
(B) 
(C) 
(D) 
Na Figura 3, está representado, no plano complexo, a sombreado, um setor circular.
Sabe-se que:
• o ponto  é a imagem geométrica do número complexo
é a imagem geométrica do número complexo 
• o ponto  tem abcissa negativa, ordenada nula, e pertence À circunferência de centro na origem do referencial e raio igual a
tem abcissa negativa, ordenada nula, e pertence À circunferência de centro na origem do referencial e raio igual a 

Qual das condições seguintes define, em 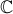 , a região a sombreado, incluindo a fronteira?
, a região a sombreado, incluindo a fronteira?
(Considere como  a determinação que pertence ao intervalo
a determinação que pertence ao intervalo  )
)
(A) 
(B) 
(C) 
(D) 
Exame Nacional de Matemática 12º Ano 2ª Fase 2011 - Grupo 1 - Exercício 7→
Na Figura 2, está representado, num referencial o. n.  , o círculo trigonométrico.
, o círculo trigonométrico.

Sabe-se que:
• 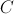 é o ponto de coordenadas
é o ponto de coordenadas 
• os pontos 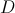 e
e  pertencem ao eixo
pertencem ao eixo 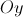
• ![\left[ {AB} \right] \left[ {AB} \right]](/images/jlatex/103109231bf469cee07093a66be902fa.gif) é um diâmetro do círculo trigonométrico
é um diâmetro do círculo trigonométrico
• as retas  e
e  são paralelas ao eixo
são paralelas ao eixo 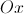
•  é a amplitude do ângulo
é a amplitude do ângulo 
• ![\theta \in \left] {0,\frac{\pi }{2}} \right[ \theta \in \left] {0,\frac{\pi }{2}} \right[](/images/jlatex/56b7f71b993d164029eb68651ca622e3.gif)
Qual das expressões seguintes dá o perímetro da região sombreada na Figura 2?
(A) 
(B) 
(C) 
(D) 
Para um certo número real positivo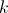 , a função
, a função  definida em
definida em  por:
por:

é contínua.
Qual é o valor de 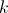 ?
?
(A) ![\sqrt[3]{e} \sqrt[3]{e}](/images/jlatex/fbf1ec86e8fd79251b9fa5725d7b74d7.gif)
(B) 
(C) 
(D) 
Exame Nacional de Matemática 12º Ano 2ª Fase 2011 - Grupo 1 - Exercício 5→