Exame Nacional de Matemática 12º Ano 2ª Fase 2011 - Grupo 1 - Exercício 7

Na Figura 3, está representado, no plano complexo, a sombreado, um setor circular.

Sabe-se que:
• o ponto é a imagem geométrica do número complexo $- \sqrt 3 + i$
• o ponto tem abcissa negativa, ordenada nula, e pertence À circunferência de centro na origem do referencial e raio igual a $\overline {OA}$

exame 2011 f2 exercicio7

Qual das condições seguintes define, em 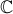$\mathbb{C}$ , a região a sombreado, incluindo a fronteira?

(Considere como $\arg \left( z \right)$ a determinação que pertence ao intervalo $\left[ {0,2\pi } \right[$ )

(A) $\left| z \right| \leqslant 2{\text{ }} \wedge {\text{ }}\frac{{2\pi }}{3} \leqslant \arg \left( z \right) \leqslant \pi$

(B) $\left| z \right| \leqslant 2{\text{ }} \wedge {\text{ }}\frac{{5\pi }}{6} \leqslant \arg \left( z \right) \leqslant \pi$

(C) $\left| z \right| \leqslant 4{\text{ }} \wedge {\text{ }}\frac{{2\pi }}{3} \leqslant \arg \left( z \right) \leqslant \pi$

(D) $\left| z \right| \leqslant 4{\text{ }} \wedge {\text{ }}\frac{{5\pi }}{6} \leqslant \arg \left( z \right) \leqslant \pi$