Exame Nacional de Matemática 12º Ano 1ª Fase 2012 - Grupo 2 - Exercício 6
Na Figura 5, está representado um trapézio retângulo ![\left[ {ABCD} \right] \left[ {ABCD} \right]](/images/jlatex/7c39be72ce8fa6c0bf88b67de000cf8a.gif) .
.
Sabe-se que:
• 
• 
• 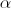 é a amplitude, em radianos, do ângulo
é a amplitude, em radianos, do ângulo 
• ![\alpha \in \left] {\frac{\pi }{2},\pi } \right[ \alpha \in \left] {\frac{\pi }{2},\pi } \right[](/images/jlatex/629dd1fb1642f9bf0c494edbf9ee3d13.gif)
Resolva os itens seguintes, recorrendo a métodos exclusivamente analíticos.
1. Mostre que o perímetro do trapézio ![\left[ {ABCD} \right] \left[ {ABCD} \right]](/images/jlatex/7c39be72ce8fa6c0bf88b67de000cf8a.gif) é dado, em função de
é dado, em função de 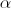 , por
, por
 .
.
2. Para um certo número real  , tem-se que
, tem-se que  , com
, com  .
.
Determine o valor exato de  .
.
Comece por mostrar que  .
.


 , de domínio
, de domínio  , definida por:
, definida por: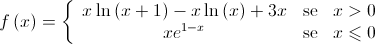
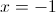 .
. , de domínio
, de domínio ![\left] {0, + \infty } \right[ \left] {0, + \infty } \right[](/images/jlatex/2631d35d1244d95aa0e498635fa2d286.gif) , definidas por:
, definidas por: e
e 
 é o único zero da função
é o único zero da função  , os gráficos das funções
, os gráficos das funções ![\left[ {OAB} \right] \left[ {OAB} \right]](/images/jlatex/4985071c7575856642f0b0d086715c52.gif) .
. é a origem do referencial;
é a origem do referencial; e
e  são pontos do gráfico de
são pontos do gráfico de 
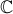 , conjunto dos números complexos, considere
, conjunto dos números complexos, considere 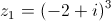 e
e 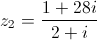 .
.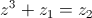 , sem recorrer à calculadora.
, sem recorrer à calculadora.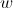 um número complexo não nulo.
um número complexo não nulo.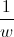 são raízes de índice
são raízes de índice 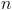 de um mesmo número complexo
de um mesmo número complexo  , então
, então 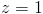 ou
ou 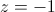 .
.
 é a imagem geométrica do complexo
é a imagem geométrica do complexo ;
; é paralela ao eixo real;
é paralela ao eixo real; a determinação que
a determinação que .
.




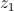 ,
, 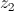 ,
,  e
e  .
. ?
?
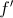 e
e 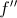 , de domínio
, de domínio 



 parte do gráfico de uma função
parte do gráfico de uma função  ,
, .
. , a função
, a função  .
.