Resolução do exercício de matemática:
1.





![\Leftrightarrow {z^3} = 8\operatorname{cis} 0 \Leftrightarrow z = \sqrt[3]{8}\operatorname{cis} \frac{{0 + 2k\pi }}{3},k \in \left\{ {0,1,2} \right\} \Leftrightarrow \Leftrightarrow {z^3} = 8\operatorname{cis} 0 \Leftrightarrow z = \sqrt[3]{8}\operatorname{cis} \frac{{0 + 2k\pi }}{3},k \in \left\{ {0,1,2} \right\} \Leftrightarrow](/images/jlatex/2badb36b49f2f7df1c8ea66f85da671d.gif)

Para  ,
, 
Para  ,
, 
Para  ,
, 
2.



Em 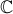 , conjunto dos números complexos, considere
, conjunto dos números complexos, considere 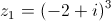 e
e 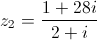 .
.
1. Resolva a equação 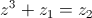 , sem recorrer à calculadora.
, sem recorrer à calculadora.
Apresente as soluções da equação na forma trigonométrica.
2. Seja 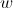 um número complexo não nulo.
um número complexo não nulo.
Mostre que, se 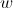 e
e 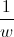 são raízes de índice
são raízes de índice 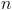 de um mesmo número complexo
de um mesmo número complexo  , então
, então 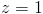 ou
ou 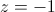 .
.