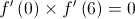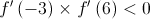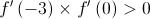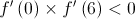Exame Nacional de Matemática 12º Ano 1ª Fase 2011 - Grupo 2 - Exercício 7
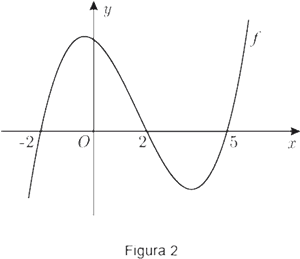
Na Figura 6, está representada, num referencial o. n.  , parte do gráfico da função
, parte do gráfico da função  .
.

Sabe-se que:
•  é uma função contínua em
é uma função contínua em 
•  não tem zeros
não tem zeros
• a segunda derivada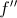 , de uma certa função
, de uma certa função  tem domínio
tem domínio 
e é definida por 
• 
Apenas uma das opções seguintes pode representar a função  .
.

Elabore uma composição na qual:
• indique a opção que pode representar 
• apresente as razões que o levam a rejeitar as restantes opções
Apresente três razões, uma por cada gráfico rejeitado.
Exame Nacional de Matemática 12º Ano 1ª Fase 2011 - Grupo 2 - Exercício 7→


 .
. e
e 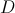 do trapézio
do trapézio![\left[ {ABCD} \right] \left[ {ABCD} \right]](/images/jlatex/7c39be72ce8fa6c0bf88b67de000cf8a.gif) pertencem ao eixo
pertencem ao eixo 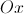
 do trapézio
do trapézio 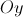
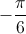
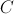 pertencem ao gráfico de
pertencem ao gráfico de 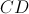 á paralela ao eixo
á paralela ao eixo 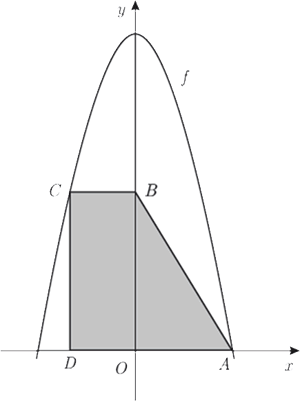
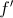 a primeira derivada da função
a primeira derivada da função 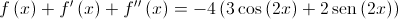 para qualquer número real
para qualquer número real 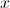 .
. .
. o ponto de interseção dessa assíntota com a reta tangente ao gráfico
o ponto de interseção dessa assíntota com a reta tangente ao gráfico .
.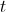 horas após as zero horas do dia 1 de Abril de 2010, é dada, aproximadamente, por
horas após as zero horas do dia 1 de Abril de 2010, é dada, aproximadamente, por , com
, com![t \in \left[ {0,20} \right] t \in \left[ {0,20} \right]](/images/jlatex/ebd251221fca80cf7138e1bd16eb7ca2.gif)
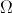 o espaço de resultados associado a uma certa experiência aleatória, e sejam
o espaço de resultados associado a uma certa experiência aleatória, e sejam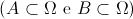 , com
, com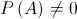 .
. .
.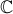 , conjunto dos números complexos, considere
, conjunto dos números complexos, considere ,
, e
e
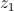 é raiz do polinómio
é raiz do polinómio .
.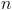 natural para o qual a imagem geométrica de
natural para o qual a imagem geométrica de , no plano complexo, está no terceiro quadrante e pertence à bissetriz dos quadrantes ímpares.
, no plano complexo, está no terceiro quadrante e pertence à bissetriz dos quadrantes ímpares.![\left[ {AB} \right] \left[ {AB} \right]](/images/jlatex/103109231bf469cee07093a66be902fa.gif) é um dos lados de um polígono regular cujos vértices são as imagens geométricas das raízes de índice 5 do complexo
é um dos lados de um polígono regular cujos vértices são as imagens geométricas das raízes de índice 5 do complexo ;
; está contido na circunferência de centro na origem do referencial e raio igual a
está contido na circunferência de centro na origem do referencial e raio igual a .
.
 ?
?



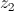 ,
, e
e .
.
 , pode ser igual a
, pode ser igual a ?
?