Atividades Educativas

Atividades Para Imprimir

Exercícios de Matemática

Jogos de Matematica

Exames de Matemática

Exames de Matemática A12º ANO

Exames de Matemática B10º ANO e 11º ANO

Exame Nacional de Matemática 12º Ano 1ª Fase 2011 - Grupo 2 - Exercício 6

Na Figura 5, está representada, num referencial o. n. xOy , parte do gráfico da função , de domínio $\mathbb{R}$ , definida por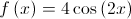 $f\left( x \right) = 4\cos \left( {2x} \right)$ .

Sabe-se que:

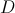• os vértices e do trapézio $\left[ {ABCD} \right]$ pertencem ao eixo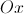

• o vértice do trapézio $\left[ {ABCD} \right]$ pertence ao eixo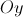

• o vértice 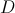do trapézio $\left[ {ABCD} \right]$ tem abcissa $- \frac{\pi }{6}$

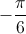
• os pontos 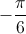$- \frac{\pi }{6}$ e 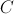pertencem ao gráfico de

• a reta 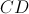á paralela ao eixo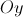

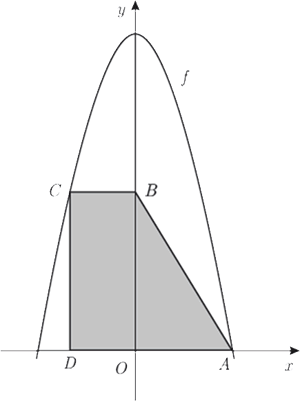
exame g2 exercicio6 01

Resolva os dois itens seguintes recorrendo a métodos exclusivamente analíticos.

Determine o valor exato da área do trapézio $\left[ {ABCD} \right]$ .

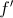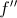Seja a primeira derivada da função , e seja f'' a segunda derivada da função .

Mostre que , 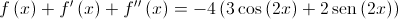$f\left( x \right) + f'\left( x \right) + f''\left( x \right) = - 4\left( {3\cos \left( {2x} \right) + 2\operatorname{sen} \left( {2x} \right)} \right)$ para qualquer número real .

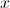Resolução do Exercício:

Determinar a abcissa do ponto A:

$f\left( x \right) = 0 \Leftrightarrow 4\cos \left( {2x} \right) = 0 \Leftrightarrow \cos \left( {2x} \right) = 0 \Leftrightarrow \cos \left( {2x} \right) = \cos \left( {\frac{\pi }{2}} \right) \Leftrightarrow$

$\Leftrightarrow 2x = \frac{\pi }{2} + 2k\pi \vee 2x = - \frac{\pi }{2} + 2k\pi ,k \in \mathbb{Z} \Leftrightarrow$

$\Leftrightarrow x = \frac{\pi }{4} + k\pi \vee x = - \frac{\pi }{4} + k\pi ,k \in \mathbb{Z}$

Se k = 0 , $\Leftrightarrow x = \frac{\pi }{4} \vee x = - \frac{\pi }{4}$

Logo, a abcissa do ponto A é $\frac{\pi }{4}$ (é o menor zero positivo de ).

• $\overline {AD} = \frac{\pi }{6} + \frac{\pi }{4} = \frac{{5\pi }}{{12}}$

• $\overline {BC} = \frac{\pi }{6}$

• Determinar a ordenada de C:

$f\left( { - \frac{\pi }{6}} \right) = 4\cos \left( { - \frac{\pi }{3}} \right) = 4 \times \frac{1}{2} = 2$

Logo, $C\left( { - \frac{\pi }{6},2} \right)$ .

Determinar a área do trapézio:

$A = \frac{{\frac{{5\pi }}{{12}} + \frac{\pi }{6}}}{2} \times 2 = \frac{{7\pi }}{{12}}$

$f'\left( x \right) = 4 \times 2 \times \left( { - \operatorname{sen} \left( {2x} \right)} \right) = - 8\operatorname{sen} \left( {2x} \right)$

$f''\left( x \right) = - 8 \times 2 \times \cos \left( {2x} \right) = - 16\cos \left( {2x} \right)$

$f\left( x \right) + f'\left( x \right) + f''\left( x \right) = 4\cos \left( {2x} \right) - 8\operatorname{sen} \left( {2x} \right) - 16\cos \left( {2x} \right) =$

$= - 12\cos \left( {2x} \right) - 8\operatorname{sen} \left( {2x} \right) = - 4\left( {3\cos \left( {2x} \right) + 2\operatorname{sen} \left( {2x} \right)} \right)$ c.q.d.