Exame Nacional de Matemática 12º Ano 1ª Fase 2011 - Grupo 2 - Exercício 4

Num museu, a temperatura ambiente em graus centígrados,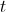 horas após as zero horas do dia 1 de Abril de 2010, é dada, aproximadamente, por

$T\left( t \right) = 15 + 0,1{t^2}{e^{ - 0,15t}}$ , com $t \in \left[ {0,20} \right]$

Determine o instante em que a temperatura atingiu o valor máximo recorrendo a métodos exclusivamente analíticos.

Resolução do Exercício:

$T'\left( t \right) = 0 + 0,2t \times {e^{ - 0,15t}} + 0,1{t^2}\left( { - 0,15 \times {e^{ - 0,15t}}} \right) = {e^{ - 0,15t}}\left( {0,2t - 0,015{t^2}} \right)$

$T'\left( t \right) = 0 \Leftrightarrow {e^{ - 0,15t}}\left( {0,2t - 0,015{t^2}} \right) = 0 \Leftrightarrow \vee 0,2t - 0,015{t^2} = 0 \Leftrightarrow$