Exame Nacional de Matemática 12º Ano 1ª Fase 2013 - Grupo 2 - Exercício 7
Considere, para um certo número real  positivo, uma função
positivo, uma função  , contínua, de domínio
, contínua, de domínio ![\left[ { - a,a} \right] \left[ { - a,a} \right]](/images/jlatex/8f7789c40e13a9d56fc3916d7d539b99.gif) .
.
Sabe-se que 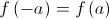 e
e 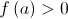 .
.
Mostre que a condição 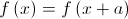 tem, pelo menos, uma solução em
tem, pelo menos, uma solução em ![\left] { - a,0} \right[ \left] { - a,0} \right[](/images/jlatex/c6c78f699a4b8bc661c121630153e0b9.gif) .
.

Considere, para um certo número real  positivo, uma função
positivo, uma função  , contínua, de domínio
, contínua, de domínio ![\left[ { - a,a} \right] \left[ { - a,a} \right]](/images/jlatex/8f7789c40e13a9d56fc3916d7d539b99.gif) .
.
Sabe-se que 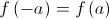 e
e 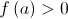 .
.
Mostre que a condição 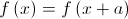 tem, pelo menos, uma solução em
tem, pelo menos, uma solução em ![\left] { - a,0} \right[ \left] { - a,0} \right[](/images/jlatex/c6c78f699a4b8bc661c121630153e0b9.gif) .
.
Considere a função  , de domínio
, de domínio ![\left] { - \frac{\pi }{2},0} \right[ \left] { - \frac{\pi }{2},0} \right[](/images/jlatex/8a319d3b118b0ff9d944869cbdf53ac2.gif) , definida por
, definida por 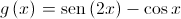 .
.
Seja  um número real do domínio de
um número real do domínio de  .
.
A reta tangente ao gráfico da função  no ponto de abcissa
no ponto de abcissa  é paralela à reta de equação
é paralela à reta de equação 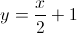 .
.
Determine o valor de  , recorrendo a métodos analíticos, sem utilizar a calculadora.
, recorrendo a métodos analíticos, sem utilizar a calculadora.
Na figura 2, está representada, num referencial ortogonal  , parte do gráfico de uma função polinomial
, parte do gráfico de uma função polinomial  , de grau 3.
, de grau 3.

Sabe-se que:
 ;
;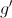 a primeira derivada de uma certa função
a primeira derivada de uma certa função  , tem domínio
, tem domínio  e é definida por
e é definida por  ;
;![\mathop {\lim }\limits_{x \to + \infty } \left[ {g\left( x \right) - 2} \right] = 0 \mathop {\lim }\limits_{x \to + \infty } \left[ {g\left( x \right) - 2} \right] = 0](/images/jlatex/02a23653e316404f0ca219db677627d3.gif) .
.Apenas uma das opções seguintes pode representar a função  .
.

Nota - Em cada uma das opções estão representadas parte do gráfico de uma função e, a tracejado, uma assíntota desse gráfico.
Elabore uma composição na qual:
 ;
;Apresente três razões diferentes, uma por cada gráfico rejeitado.
Exame Nacional de Matemática 12º Ano 1ª Fase 2013 - Grupo 2 - Exercício 5→
Considere a função  , de domínio
, de domínio 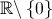 , definida por:
, definida por:
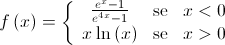
Resolva os itens 4.1. e 4.2., recorrendo a métodos analíticos, sem utilizar a calculadora.
1. Estude a função  quanto à existência de assíntotas verticais do seu gráfico.
quanto à existência de assíntotas verticais do seu gráfico.
2. Seja  a função, de domínio
a função, de domínio 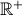 , definida por
, definida por 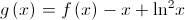 .
.
Estude a função quanto à monotonia e quanto à existência de extremos relativos em ![\left] {0,e} \right] \left] {0,e} \right]](/images/jlatex/2d01e4d43af8aa394cf3389db4956f0c.gif) .
.
3. Resolva este item recorrendo à calculadora.
Considere num referencial o.n.  , a representação gráfica da função
, a representação gráfica da função  , de domínio
, de domínio 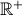 , definida por
, definida por 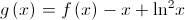 .
.
Sabe-se que:
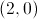
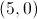
 .
.Para cada posição do ponto P, considere o triângulo [ABP].
Determine as abcissas dos pontos P para os quais a área do triângulo [ABP] é 1.
Na sua resposta, deve:
Seja 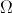 o espaço de resultados associado a uma certa experiência aleatória.
o espaço de resultados associado a uma certa experiência aleatória.
Sejam  e
e  dois acontecimentos (
dois acontecimentos (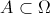 e
e 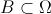 ).
).
Sabe-se que:



Determine  .
.
Uma caixa contém apenas bolas brancas e bolas pretas, indistinguíveis ao tato.
Todas as bolas estão numeradas com um único número natural.
Sabe-se que:
 das bolas pretas têm um número par;
das bolas pretas têm um número par; das bolas brancas têm um número ímpar.
das bolas brancas têm um número ímpar.
1. Retira-se, ao acaso, uma bola dessa caixa.
Determine a probabilidade de essa bola ser preta, sabendo que tem um número par.
Apresente o resultado na forma de fração irredutível.
2. Admita agora que a caixa tem 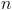 bolas.
bolas.
Extraem-se, ao acaso, sucessivamente e sem reposição, duas bolas da caixa.
Determine 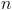 , sabendo que a probabilidade de ambas as bolas serem brancas é igual a
, sabendo que a probabilidade de ambas as bolas serem brancas é igual a  .
.
Em 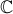 , conjunto dos números complexos, considere
, conjunto dos números complexos, considere  e
e  .
.
1. Sabe-se que  é uma raiz quarta de um certo número complexo
é uma raiz quarta de um certo número complexo 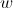 .
.
Determine 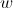 na forma algébrica, sem utilizar a calculadora.
na forma algébrica, sem utilizar a calculadora.
2. Seja  .
.
Determine o valor de 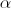 pertencente ao intervalo
pertencente ao intervalo ![\left] { - 2\pi , - \pi } \right[ \left] { - 2\pi , - \pi } \right[](/images/jlatex/0ecddd53e4514b94361519d5d496f99b.gif) , sabendo que
, sabendo que  é um número real.
é um número real.
Exame Nacional de Matemática 12º Ano 1ª Fase 2013 - Grupo 2 - Exercício 1→
Em 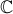 , conjunto dos números complexos, considere
, conjunto dos números complexos, considere  e
e  .
.
Seja 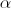 um argumento do número complexo
um argumento do número complexo  .
.
Qual das opções seguintes é verdadeira?
(A) 
(B) 
(C) 
(D) 
Na Figura 1, estão representadas, no plano complexo, as imagens geométricas de quatro números complexos:  ,
,  ,
,  e
e  .
.

Qual é o número complexo que, com  , pode ser igual a
, pode ser igual a  ?
?
(A) 
(B) 
(C) 
(D) 
Considere, para um certo número real  superior a 1, as funções
superior a 1, as funções  e
e  , de domínio
, de domínio  , definidas por
, definidas por  e
e  .
.
Considere as afirmações seguintes.
I) Os gráficos das funções  e
e  não se intersectam.
não se intersectam.
II) As funções  e
e  são monótonas crescentes.
são monótonas crescentes.
III)  .
.
Qual das opções seguintes é a correta?
(A) I e III são verdadeiras.
(B) I é falsa e III é verdadeira.
(C) I é verdadeira e III é falsa.
(D) II e III são falsas.
Exame Nacional de Matemática 12º Ano 1ª Fase 2013 - Grupo 1 - Exercício 6→