Exame Nacional de Matemática 12º Ano 1ª Fase 2013 - Grupo 2 - Exercício 1

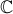Em $\mathbb{C}$ , conjunto dos números complexos, considere ${z_1} = \sqrt 2 + 2\operatorname{cis} \frac{{3\pi }}{4}$ e ${z_2} = 1 + i$ .

1. Sabe-se que $\frac{{{z_1}}}{{{z_2}}}$ é uma raiz quarta de um certo número complexo .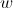

Determine 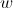na forma algébrica, sem utilizar a calculadora.

2. Seja ${z_3} = \operatorname{cis} \alpha$ .

Determine o valor de 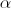$\alpha$ pertencente ao intervalo $\left] { - 2\pi , - \pi } \right[$ , sabendo que ${z_3} + \overline {{z_2}}$ é um número real.

Resolução do exercício de matemática:

1. ${z_1} = \sqrt 2 + 2\operatorname{cis} \frac{{3\pi }}{4} = \sqrt 2 + 2\left( {\cos \frac{{3\pi }}{4} + i\operatorname{sen} \frac{{3\pi }}{4}} \right) =$ $= \sqrt 2 + 2\left( { - \frac{{\sqrt 2 }}{2} + \frac{{\sqrt 2 }}{2}i} \right) = = \sqrt 2 - \sqrt 2 + \sqrt 2 i = \sqrt 2 i =$ $= \sqrt 2 \operatorname{cis} \frac{\pi }{2}$ ${z_2} = 1 + i = \sqrt 2 \operatorname{cis} \frac{\pi }{4}$ $\left| {{z_2}} \right| = \sqrt {{1^2} + {1^2}} = \sqrt 2$ $\operatorname{tg} \theta = \frac{1}{1} \wedge \theta \in 1.Q \Rightarrow \theta = \frac{\pi }{4}$ $\frac{{{z_1}}}{{{z_2}}} = \frac{{\sqrt 2 \operatorname{cis} \frac{\pi }{2}}}{{\sqrt 2 \operatorname{cis} \frac{\pi }{4}}} = \frac{{\sqrt 2 }}{{\sqrt 2 }}\operatorname{cis} \left( {\frac{\pi }{2} - \frac{\pi }{4}} \right) = \operatorname{cis} \frac{\pi }{4}$ $w = {\left( {\frac{{{z_1}}}{{{z_2}}}} \right)^4} = {\left( {\operatorname{cis} \frac{\pi }{4}} \right)^4} = \operatorname{cis} \left( {4 \times \frac{\pi }{4}} \right) = \operatorname{cis} \pi = - 1$

2. ${z_3} + \overline {{z_2}} = \operatorname{cis} \alpha + 1 - i = \cos \alpha + i\operatorname{sen} \alpha + 1 - i = \cos \alpha + 1 + \left( {\operatorname{sen} \alpha - 1} \right)i$

${z_3} + \overline {{z_2}}$ é um número real se:

$\operatorname{sen} \alpha - 1 = 0 \Leftrightarrow \operatorname{sen} \alpha = 1 \Leftrightarrow \alpha = - \frac{{3\pi }}{2}$ (porque $\alpha \in \left] { - 2\pi , - \pi } \right[$ ).