Solução: (D)



Logo, a assíntota tem declive 3.
Logo, a equação pretendida é  .
.
Seja  uma função de domínio
uma função de domínio 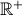 .
.
Sabe-se que  .
.
Qual das equações seguintes pode definir uma assíntota do gráfico da função  ?
?
(A) 
(B) 
(C) 
(D) 
Solução: (D)



Logo, a assíntota tem declive 3.
Logo, a equação pretendida é  .
.