Numa conferência de imprensa, estiveram presentes 20 jornalistas.
3.1. Considere a experiência aleatória que consiste em escolher, ao acaso, um dos 20 jornalistas presentes nessa
conferência de imprensa.
Seja X a variável aleatória «número de jornalistas do sexo feminino escolhidos».
A tabela de distribuição de probabilidades da variável X é a seguinte:
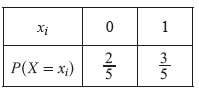
Considere agora a experiência aleatória que consiste em escolher, ao acaso, dois dos 20 jornalistas presentes nessa
conferência de imprensa.
Seja Y a variável aleatória «número de jornalistas do sexo feminino escolhidos».
Construa a tabela de distribuição de probabilidades da variável Y.
Apresente as probabilidades na forma de fração.
3.2. Considere o problema seguinte.
«Admita que a conferência de imprensa se realiza numa sala, cujas cadeiras se encontram dispostas em cinco filas,
cada uma com oito cadeiras. Todos os jornalistas se sentam, não mais do que um em cada cadeira, nas três
primeiras filas.
De quantas maneiras diferentes se podem sentar os 20 jornalistas, sabendo que as duas primeiras filas devem ficar
totalmente ocupadas?»
Apresentam-se, em seguida, duas respostas corretas.
Resposta I) 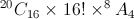 Resposta II)
Resposta II) 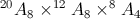
Numa composição, apresente os raciocínios que conduzem a cada uma dessas respostas.
Exame Nacional de Matemática 12º Ano 2ª Fase 2013 - Grupo 2 - Exercício 3→
 , o triângulo [OAB] e a reta
, o triângulo [OAB] e a reta 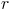 .
.

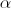 , por
, por  .
. no ponto de abcissa
no ponto de abcissa  , sem utilizar a calculadora.
, sem utilizar a calculadora. 

 , de domínio [- 1,2], definida por
, de domínio [- 1,2], definida por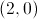 e um ponto P que se desloca ao longo do gráfico da função
e um ponto P que se desloca ao longo do gráfico da função  uma função, de domínio
uma função, de domínio 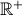 , cuja derivada,
, cuja derivada, 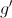 , de domínio
, de domínio 
 , definida por:
, definida por:
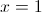 .
. tende para
tende para  .
.
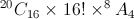 Resposta II)
Resposta II) 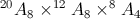



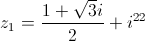 e
e 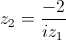 .
.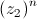 é um número real negativo.
é um número real negativo.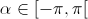 .
.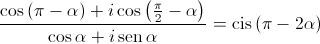 .
. , conjunto dos números complexos,a condição
, conjunto dos números complexos,a condição
 a determinação que pertence ao intervalo
a determinação que pertence ao intervalo  .
.
 , com
, com  .
.![\alpha \in \left] {0,\frac{\pi }{2}} \right[ \alpha \in \left] {0,\frac{\pi }{2}} \right[](/images/jlatex/69c94243be204049f124771bf16c84d9.gif) .
. ?
?




 .
. , primeira derivada da função
, primeira derivada da função