Considere num referencial o.n.  , a representação gráfica da função
, a representação gráfica da função  , de domínio [- 1,2], definida por
, de domínio [- 1,2], definida por

o ponto A de coordenadas 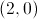 e um ponto P que se desloca ao longo do gráfico da função
e um ponto P que se desloca ao longo do gráfico da função  .
.
Existe uma posição do ponto P para a qual a área do triângulo [AOP] é mínima.
Determine a área desse triângulo, recorrendo à calculadora gráfica.
Na sua resposta, deve:
- reproduzir o gráfico da função ou os gráficos das funções que tiver necessidade de visualizar na calculadora, devidamente identificado(s), incluindo o referencial;
- indicar o valor da área do triângulo [AOP] com arredondamento às centésimas.
Resolução do exercício de matemática:
A área do triângulo [AOP] é mínima quando a altura do triângulo, em relação à base [OA], for mínima, o que acontece quando a ordenada do ponto P for o máximo de  , no intervalo [-1, 2].
, no intervalo [-1, 2].

P(-0,15 ; -2,92)
Logo, a área do triângulo é dada por:

 , no intervalo [-1, 2].
, no intervalo [-1, 2].


 , a representação gráfica da função
, a representação gráfica da função 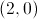 e um ponto P que se desloca ao longo do gráfico da função
e um ponto P que se desloca ao longo do gráfico da função 



