Solução: (B)
Como  , a concavidade do gráfico em
, a concavidade do gráfico em  está voltada para baixo.
está voltada para baixo.

Logo,  é um máximo relativo da função
é um máximo relativo da função  .
.
Sejam 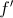 e
e 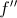 , de domínio
, de domínio  , a primeira derivada e a segunda derivada de uma função
, a primeira derivada e a segunda derivada de uma função  , respetivamente.
, respetivamente.
Sabe-se que:
 é um número real;
é um número real; de abcissa
de abcissa 


Qual das afirmações seguintes é necessariamente verdadeira?
(A)  é um zero da função
é um zero da função 
(B)  é um máximo relativo da função
é um máximo relativo da função 
(C)  é um mínimo relativo da função
é um mínimo relativo da função 
(D) P é o ponto de inflexão do gráfico da função 
Solução: (B)
Como  , a concavidade do gráfico em
, a concavidade do gráfico em  está voltada para baixo.
está voltada para baixo.

Logo,  é um máximo relativo da função
é um máximo relativo da função  .
.