Resolução do exercício de matemática:
1.1.








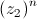 é um número real negativo se:
é um número real negativo se:


Para  , obtemos
, obtemos  .
.
Logo,  .
.
1.2.


1.1. Considere 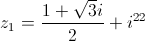 e
e 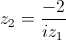 .
.
Determine, sem utilizar a calculadora, o menor número natural n tal que 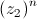 é um número real negativo.
é um número real negativo.
1.2. Seja 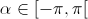 .
.
Mostre que 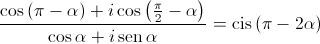 .
.
Resolução do exercício de matemática:
1.1.








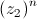 é um número real negativo se:
é um número real negativo se:


Para  , obtemos
, obtemos  .
.
Logo,  .
.
1.2.

