Considere a função  , de domínio
, de domínio 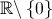 , definida por:
, definida por:
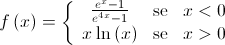
Resolva os itens 4.1. e 4.2., recorrendo a métodos analíticos, sem utilizar a calculadora.
1. Estude a função  quanto à existência de assíntotas verticais do seu gráfico.
quanto à existência de assíntotas verticais do seu gráfico.
2. Seja  a função, de domínio
a função, de domínio 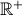 , definida por
, definida por 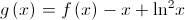 .
.
Estude a função quanto à monotonia e quanto à existência de extremos relativos em ![\left] {0,e} \right] \left] {0,e} \right]](/images/jlatex/2d01e4d43af8aa394cf3389db4956f0c.gif) .
.
3. Resolva este item recorrendo à calculadora.
Considere num referencial o.n.  , a representação gráfica da função
, a representação gráfica da função  , de domínio
, de domínio 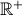 , definida por
, definida por 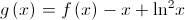 .
.
Sabe-se que:
- A é o ponto de coordenadas
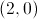
- B é o ponto de coordenadas
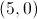
- P é um ponto que se desloca ao longo do gráfico da função
 .
.
Para cada posição do ponto P, considere o triângulo [ABP].
Determine as abcissas dos pontos P para os quais a área do triângulo [ABP] é 1.
Na sua resposta, deve:
- equacionar o problema;
- reproduzir o gráfico da função ou os gráficos das funções que tiver necessidade de visualizar na calculadora, devidamente identificado(s), incluindo o referencial;
- indicar as coordenadas dos pontos P com arredondamento às centésimas.
Exercicios de Matematica 12 ANO - Função definida por ramos - Exercício 1→
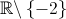 , definida por
, definida por 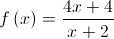 .
.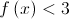 .
. .
. com os eixos coordenados.
com os eixos coordenados.


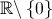 , definida por:
, definida por: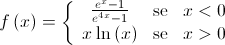
 a função, de domínio
a função, de domínio 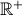 , definida por
, definida por 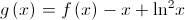 .
.![\left] {0,e} \right] \left] {0,e} \right]](/images/jlatex/2d01e4d43af8aa394cf3389db4956f0c.gif) .
. , a representação gráfica da função
, a representação gráfica da função 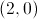
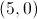
 , definida por:
, definida por: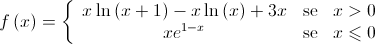
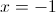 .
.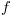 , de domínio
, de domínio 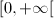 , definida por
, definida por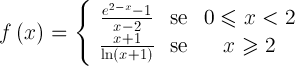
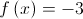 tem, pelo menos, uma solução em
tem, pelo menos, uma solução em ![\left] {0,\frac{1}{2}} \right[ \left] {0,\frac{1}{2}} \right[](/images/jlatex/3a22da03bfe5e59c313c4ed2e8900ff7.gif) .
.![\left] {2, + \infty } \right[ \left] {2, + \infty } \right[](/images/jlatex/aba2e90d9254a962a10b0d0dbae4eefa.gif) .
.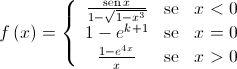
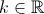 .
.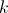 , de modo que
, de modo que 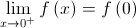 .
.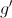 , de domínio
, de domínio 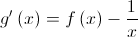 .
.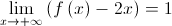
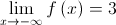
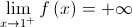
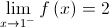
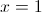 e
e 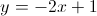
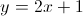
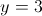 e
e 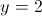 e
e