Resolução do Exercício de Matemática:
1.1. 




![S = \left] { - 2,2} \right[ S = \left] { - 2,2} \right[](/images/jlatex/3905686b5e84bced1bd94cc245e1f5ac.gif)
1.2.


Equação da assíntota vertical: x = - 2
Equação da assíntota horizontal: y = 4
1.3. 
Coordenadas do ponto de interseção com o eixo Oy: (0, 2)


Coordenadas do ponto de interseção com o eixo Ox: (-1, 0)

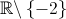 , definida por
, definida por 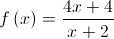 .
.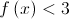 .
. .
.