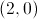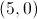Considere a função  , de domínio
, de domínio 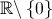 , definida por:
, definida por:
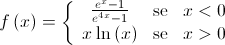
Resolva os itens 4.1. e 4.2., recorrendo a métodos analíticos, sem utilizar a calculadora.
1. Estude a função  quanto à existência de assíntotas verticais do seu gráfico.
quanto à existência de assíntotas verticais do seu gráfico.
2. Seja  a função, de domínio
a função, de domínio 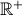 , definida por
, definida por 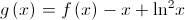 .
.
Estude a função quanto à monotonia e quanto à existência de extremos relativos em ![\left] {0,e} \right] \left] {0,e} \right]](/images/jlatex/2d01e4d43af8aa394cf3389db4956f0c.gif) .
.
3. Resolva este item recorrendo à calculadora.
Considere num referencial o.n.  , a representação gráfica da função
, a representação gráfica da função  , de domínio
, de domínio 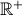 , definida por
, definida por 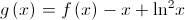 .
.
Sabe-se que:
- A é o ponto de coordenadas
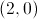
- B é o ponto de coordenadas
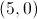
- P é um ponto que se desloca ao longo do gráfico da função
 .
.
Para cada posição do ponto P, considere o triângulo [ABP].
Determine as abcissas dos pontos P para os quais a área do triângulo [ABP] é 1.
Na sua resposta, deve:
- equacionar o problema;
- reproduzir o gráfico da função ou os gráficos das funções que tiver necessidade de visualizar na calculadora, devidamente identificado(s), incluindo o referencial;
- indicar as coordenadas dos pontos P com arredondamento às centésimas.
Resolução do exercício de matemática:
1. 

Mudança de variável:  (quando
(quando  ,
,  ).
).

(quando  ,
,  ).
).
Logo, a reta de equação  não é assíntota vertical do gráfico de
não é assíntota vertical do gráfico de  .
.
Como  é contínua em
é contínua em 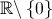 , o gráfico de
, o gráfico de  não admite outras assíntotas verticais.
não admite outras assíntotas verticais.
2.







Em ![\left] {0,e} \right] \left] {0,e} \right]](/images/jlatex/2d01e4d43af8aa394cf3389db4956f0c.gif) , o único zero de
, o único zero de 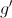 é
é 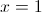 .
.



A função  é estritamente decrescente em
é estritamente decrescente em ![\left] {0,1} \right] \left] {0,1} \right]](/images/jlatex/acaeaed109c5c7c40b4a0f0347d97bcd.gif) e estritamente decrescente em
e estritamente decrescente em ![\left[ {1,e} \right] \left[ {1,e} \right]](/images/jlatex/b6a2da9d61c39be304191f99965040dc.gif) .
.
 tem um mínimo relativo igual a
tem um mínimo relativo igual a  para
para 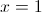 e um máximo relativo igual a
e um máximo relativo igual a  para
para  .
.
3.
Queremos determinar os valores de  tais que:
tais que:



As abcissas dos pontos P são:  .
.


 (quando
(quando  ,
,  ).
).
 ,
,  ).
). não é assíntota vertical do gráfico de
não é assíntota vertical do gráfico de  .
. é contínua em
é contínua em 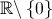 , o gráfico de
, o gráfico de  não admite outras assíntotas verticais.
não admite outras assíntotas verticais.






![\left] {0,e} \right] \left] {0,e} \right]](/images/jlatex/2d01e4d43af8aa394cf3389db4956f0c.gif) , o único zero de
, o único zero de 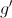 é
é 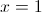 .
.


 é estritamente decrescente em
é estritamente decrescente em ![\left] {0,1} \right] \left] {0,1} \right]](/images/jlatex/acaeaed109c5c7c40b4a0f0347d97bcd.gif) e estritamente decrescente em
e estritamente decrescente em ![\left[ {1,e} \right] \left[ {1,e} \right]](/images/jlatex/b6a2da9d61c39be304191f99965040dc.gif) .
. tem um mínimo relativo igual a
tem um mínimo relativo igual a  para
para 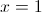 e um máximo relativo igual a
e um máximo relativo igual a  para
para  .
. tais que:
tais que: 


 .
.
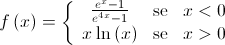
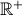 , definida por
, definida por 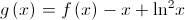 .
. , a representação gráfica da função
, a representação gráfica da função