Exame Nacional de Matemática 12º Ano 1ª Fase 2014 - Grupo 2 - Exercício 7
Considere a função  , de domínio
, de domínio ![\left] { - {e^2}, + \infty } \right[ \left] { - {e^2}, + \infty } \right[](/images/jlatex/82c71716f0dd98bbe1a0e4708bdaade5.gif) , definida
, definida .
.
Na Figura 5, estão representados, num referencial o.n.  , parte do gráfico da função
, parte do gráfico da função  e o triângulo [ABC].
e o triângulo [ABC].

Sabe-se que:
- o ponto A tem coordenadas (0, -2);
- o ponto B pertence ao gráfico da função e tem abcissa negativa;
- o ponto C pertence ao eixo Oy e tem ordenada igual à do ponto B;
- a área do triângulo [ABC] é igual a 8.
Determine a abcissa do ponto B, recorrendo à calculadora gráfica.
Na sua resposta, deve:
- escrever uma expressão da área do triângulo [ABC] em função da abcissa do ponto B;
- equacionar o problema;
- reproduzir, num referencial, o gráfico da função ou os gráficos das funções visualizados, devidamente identificados;
- indicar a abcissa do ponto B com arredondamento às centésimas.
Exame Nacional de Matemática 12º Ano 1ª Fase 2014 - Grupo 2 - Exercício 7→


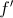 , de domínio
, de domínio  , é dada por
, é dada por  .
. .
.![\left] { - \frac{\pi }{2},\frac{\pi }{4}} \right[ \left] { - \frac{\pi }{2},\frac{\pi }{4}} \right[](/images/jlatex/3b07aac6fc2936bf16463b2b571027aa.gif) , recorrendo a métodos analíticos, sem utilizar a calculadora.
, recorrendo a métodos analíticos, sem utilizar a calculadora.
 .
.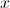 tende para
tende para  , de equação
, de equação  , com
, com  .
.  .
. , o cubo [OABCDEFG], de aresta 3.
, o cubo [OABCDEFG], de aresta 3.
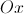
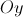

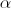 a amplitude, em radianos, do ângulo AHC.
a amplitude, em radianos, do ângulo AHC. , sem utilizar a calculadora.
, sem utilizar a calculadora.
 , sem aplicar a fórmula da probabilidade condicionada.
, sem aplicar a fórmula da probabilidade condicionada.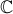 o conjunto dos números complexos.
o conjunto dos números complexos.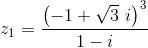 e
e 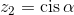 , com
, com 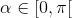 .
.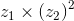 seja um número imaginário puro, sem utilizar a calculadora.
seja um número imaginário puro, sem utilizar a calculadora.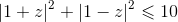 .
.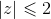 .
.
 .
.




![\alpha \in \left] {\frac{\pi }{2},\pi } \right[ \alpha \in \left] {\frac{\pi }{2},\pi } \right[](/images/jlatex/629dd1fb1642f9bf0c494edbf9ee3d13.gif) .
.



 .
.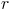 uma reta perpendicular ao plano
uma reta perpendicular ao plano