Resolução do exercício de matemática:
1.1.










Para que 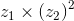 seja um número imaginário puro é necessário que:
seja um número imaginário puro é necessário que:




Resposta:  e
e  .
.
1.2.
Seja  , com
, com  .
.





Seja 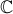 o conjunto dos números complexos.
o conjunto dos números complexos.
1.1. Considere 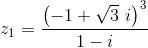 e
e 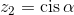 , com
, com 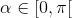 .
.
Determine os valores de 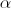 , de modo que
, de modo que 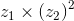 seja um número imaginário puro, sem utilizar a calculadora.
seja um número imaginário puro, sem utilizar a calculadora.
1.2. Seja z um número complexo tal que 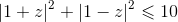 .
.
Mostre que 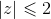 .
.
Resolução do exercício de matemática:
1.1.










Para que 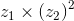 seja um número imaginário puro é necessário que:
seja um número imaginário puro é necessário que:




Resposta:  e
e  .
.
1.2.
Seja  , com
, com  .
.




