Resolução do exercício de matemática:
Solução: (C)



Seja  a função, de domínio
a função, de domínio 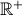 , definida por
, definida por  .
.
Considere a sucessão de números reais  tal que
tal que  .
.
Qual é o valor de  ?
?
(A) 
(B) 
(C) 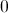
(D) 
Resolução do exercício de matemática:
Solução: (C)


