Solução: (A)
 representa a coroa circular de centro
representa a coroa circular de centro  e raios
e raios  e 3.
e 3.
 representa a região delimitada pelas semirretas com origem no ponto
representa a região delimitada pelas semirretas com origem no ponto  e que fazem ângulos de amplitudes
e que fazem ângulos de amplitudes  e
e  com a parte positiva do eixo dos
com a parte positiva do eixo dos  .
.
Logo, a opção correta é a (A).

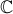 , conjunto dos números complexos,a condição
, conjunto dos números complexos,a condição
 a determinação que pertence ao intervalo
a determinação que pertence ao intervalo  .
.




