Na Figura 6, está representada, num referencial o. n.  , parte do gráfico da função
, parte do gráfico da função  .
.

Sabe-se que:
•  é uma função contínua em
é uma função contínua em 
•  não tem zeros
não tem zeros
• a segunda derivada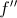 , de uma certa função
, de uma certa função  tem domínio
tem domínio 
e é definida por 
• 
Apenas uma das opções seguintes pode representar a função  .
.

Elabore uma composição na qual:
• indique a opção que pode representar 
• apresente as razões que o levam a rejeitar as restantes opções
Apresente três razões, uma por cada gráfico rejeitado.
Resolução do Exercício:
•




Logo,  em
em ![\left] {1,4} \right[ \left] {1,4} \right[](/images/jlatex/f2e09f26592828145a7fb3609035a8b0.gif) ;
;
Logo, neste intervalo a concavidade tem que estar voltada para baixo, o que não acontece no gráfico I.
• , logo,
, logo, e
e  têm que ter o mesmo sinal, o que não se verifica no gráfico II.
têm que ter o mesmo sinal, o que não se verifica no gráfico II.
• Como a função 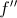 está definida em
está definida em  , então a função
, então a função  é contínua em
é contínua em  , o que não se verifica no gráfico IV.
, o que não se verifica no gráfico IV.





 em
em ![\left] {1,4} \right[ \left] {1,4} \right[](/images/jlatex/f2e09f26592828145a7fb3609035a8b0.gif) ;
; , logo,
, logo, e
e  têm que ter o mesmo sinal, o que não se verifica no gráfico II.
têm que ter o mesmo sinal, o que não se verifica no gráfico II.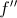 está definida em
está definida em  , então a função
, então a função  é contínua em
é contínua em  , o que não se verifica no gráfico IV.
, o que não se verifica no gráfico IV.
 , parte do gráfico da função
, parte do gráfico da função  .
.





