Exame Nacional de Matemática 12º Ano 1ª Fase 2012 - Grupo 1 - Exercício 1

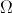Seja $\Omega$ o espaço de resultados associado a uma certa experiência aleatória, e sejam e dois acontecimentos $\left( {A \subset \Omega {\text{ e }}B \subset \Omega } \right)$ .

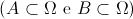Sabe-se que:

• e são acontecimentos independentes;

• $P\left( {\overline A } \right) = \frac{7}{{10}}$

• $P\left( {A \cup B} \right) = \frac{3}{4}$

Qual é o valor de $P\left( B \right)$ ?

(A) $\frac{5}{{14}}$

(B) $\frac{9}{{14}}$

(D) $\frac{{11}}{{20}}$

Resolução do exercício de matemática:

Solução: (B)

$P\left( A \right) = 1 - P\left( {\overline A } \right) = 1 - \frac{7}{{10}} = \frac{3}{{10}}$

Como A e B são independentes, então $P\left( {A \cap B} \right) = P\left( A \right) \times P\left( B \right) = \frac{3}{{10}} \times P\left( B \right)$ .

$P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cap B} \right) \Leftrightarrow \frac{3}{4} = \frac{3}{{10}} + P\left( B \right) - \frac{3}{{10}} \times P\left( B \right) \Leftrightarrow$

$\Leftrightarrow \frac{3}{4} - \frac{3}{{10}} = P\left( B \right) \times \left( {1 - \frac{3}{{10}}} \right) \Leftrightarrow \frac{{15}}{{20}} - \frac{6}{{20}} = P\left( B \right) \times \frac{7}{{10}} \Leftrightarrow$

$\Leftrightarrow \frac{9}{{20}} = P\left( B \right) \times \frac{{14}}{{20}} \Leftrightarrow 9 = 14 \times P\left( B \right) \Leftrightarrow P\left( B \right) = \frac{9}{{14}}$