Exame Nacional de Matemática 12º Ano 2ª Fase 2011 - Grupo 2 - Exercício 3

Na estufa de um certo jardim botânico, existem dois lagos aquecidos, o lago e o lago .
Às zero horas do dia 1 de março de 2010, cada lago recebeu uma espécie diferente de nenúfares, a saber, Victoria amazonica e Victoria cruziana.

${N_A}\left( t \right)$ é o número aproximado de nenúfares existentes no lago , 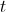dias após as zero horas do dia 1 de março de 2010. Esses nenúfares são da espécie Victoria amazonica e desenvolvem-se segundo o modelo:

${N_A}\left( t \right) = \frac{{120}}{{1 + 7 \times {e^{ - 0,2t}}}}$ , com $t \geqslant 0$

${N_B}\left( t \right)$ é o número aproximado de nenúfares existentes no lago, 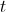dias após as zero horas do dia 1 de março de 2010. Esses nenúfares são da espécie Victoria cruziana e desenvolvem-se segundo o modelo

${N_B}\left( t \right) = \frac{{150}}{{1 + 50 \times {e^{ - 0,4t}}}}$ , com $t \geqslant 0$

Resolva os dois itens seguintes recorrendo a métodos exclusivamente analíticos.

Como foi referido, às zero horas do dia 1 de março de 2010, o lago recebeu um certo número de nenúfares da espécie Victoria amazonica. Decorridos 7 dias, esse número aumentou.

Determine de quanto foi esse aumento.

Apresente o resultado com arredondamento às unidades.

Determine quantos dias foram necessários, após as zero horas do dia 1 de março de 2010, para que o número de nenúfares existentes no lago fosse igual ao número de nenúfares existentes no lago .

Apresente o resultado com arredondamento às unidades.

Resolução do Exercício

${N_A}\left( 0 \right) = \frac{{120}}{{1 + 7 \times {e^{ - 0,2 \times 0}}}} = 15$

${N_A}\left( 7 \right) = \frac{{120}}{{1 + 7 \times {e^{ - 0,2 \times 7}}}} \simeq 44,02$

${N_A}\left( 7 \right) - {N_A}\left( 0 \right) \simeq 44 - 15 = 29$

O aumento foi de 29 nenúfares.

${N_A}\left( t \right) = {N_A}\left( t \right) \Leftrightarrow \frac{{120}}{{1 + 7 \times {e^{ - 0,2t}}}} = \frac{{150}}{{1 + 50 \times {e^{ - 0,4t}}}} \Leftrightarrow$

$\Leftrightarrow 120 + 6000{e^{ - 0,4t}} = 150 + 1050{e^{ - 0,2t}} \Leftrightarrow$

$\Leftrightarrow 6000{e^{ - 0,4t}} - 1050{e^{ - 0,2t}} - 30 = 0 \Leftrightarrow$

$\Leftrightarrow 6000{\left( {{e^{ - 0,2t}}} \right)^2} - 1050{e^{ - 0,2t}} - 30 = 0$

Fazendo $y = {e^{ - 0,2t}}$ , tem-se:

${e^{ - 0,2t}} = \frac{1}{5} \vee \mathop {{e^{ - 0,2t}} = - \frac{1}{{40}}}\limits_{{\text{equa\c{c}\~a o imposs\'i vel}}} \Leftrightarrow - 0,2t = \ln \left( {\frac{1}{5}} \right) \Leftrightarrow$

$\Leftrightarrow t = \frac{{\ln \left( {\frac{1}{5}} \right)}}{{ - 0,2}} \Leftrightarrow t \simeq 8,05$

Durante o 9º dia, o número de nenúfares do lago A iguala o número de nenúfares do lago B. Logo, só depois de 8 dias completos se dá a igualdade nos dois lagos.