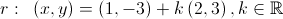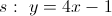Resolução do exercício de matemática:
- Escrever a equação reduzida da reta
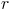 :
:
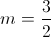
A equação reduzida da reta é do tipo: 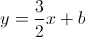 .
.
Como 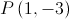 é um ponto da reta
é um ponto da reta 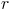 , tem-se que:
, tem-se que:
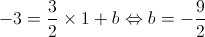
Logo, a equação reduzida da reta 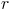 é:
é: 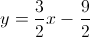 .
.
- Coordenadas do ponto de interseção das retas
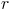 e
e 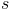 :
:
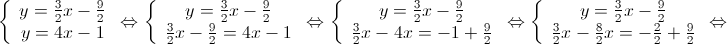
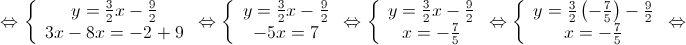
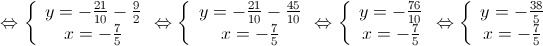
Logo, 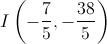 .
.