Exercicios de Matematica 11º ANO - Geometria - Atividade 1

Na Figura 4, está representado, num referencial o.n. Oxyz , o cubo [OABCDEFG], de aresta 3.

2014-f1-g2-ex4

Sabe-se que:

o ponto A pertence ao semieixo positivo
o ponto C pertence ao semieixo negativo
o ponto D pertence ao semieixo positivo
o ponto H tem coordenadas (3, -2, 3).

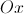
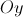
Seja 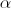$\alpha$ a amplitude, em radianos, do ângulo AHC.

Determine o valor exato de ${\operatorname{sen} ^2}\alpha$ , sem utilizar a calculadora.

Resolução do exercício de matemática:

$\overrightarrow {HA} = A - H = \left( {3,0,0} \right) - \left( {3, - 2,3} \right) = \left( {0,2, - 3} \right)$

$\overrightarrow {HC} = C - H = \left( {0, - 3,0} \right) - \left( {3, - 2,3} \right) = \left( { - 3, - 1, - 3} \right)$

$\left\| {\overrightarrow {HA} } \right\| = \sqrt {{0^2} + {2^2} + {{\left( { - 3} \right)}^2}} = \sqrt {13}$

$\left\| {\overrightarrow {HC} } \right\| = \sqrt {{{\left( { - 3} \right)}^2} + {{\left( { - 1} \right)}^2} + {{\left( { - 3} \right)}^2}} = \sqrt {19}$

$\overrightarrow {HA} .\overrightarrow {HC} = 0 \times \left( { - 3} \right) + 2 \times \left( { - 1} \right) + \left( { - 3} \right) \times \left( { - 3} \right) = 7$

$\cos \alpha = \frac{{\overrightarrow {HA} .\overrightarrow {HC} }}{{\left\| {\overrightarrow {HA} } \right\| \times \left\| {\overrightarrow {HC} } \right\|}} = \frac{7}{{\sqrt {13} \times \sqrt {19} }} = \frac{7}{{\sqrt {247} }}$

${\operatorname{sen} ^2}\alpha + {\left( {\frac{7}{{\sqrt {247} }}} \right)^2} = 1 \Leftrightarrow {\operatorname{sen} ^2}\alpha + \frac{{49}}{{247}} = 1 \Leftrightarrow {\operatorname{sen} ^2}\alpha = 1 - \frac{{49}}{{247}} \Leftrightarrow$