Na figura 2, está representada, num referencial ortogonal  , parte do gráfico de uma função polinomial
, parte do gráfico de uma função polinomial  , de grau 3.
, de grau 3.

Sabe-se que:
- -1 e 2 são os únicos zeros da função
 ;
;
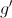 a primeira derivada de uma certa função
a primeira derivada de uma certa função  , tem domínio
, tem domínio  e é definida por
e é definida por  ;
;![\mathop {\lim }\limits_{x \to + \infty } \left[ {g\left( x \right) - 2} \right] = 0 \mathop {\lim }\limits_{x \to + \infty } \left[ {g\left( x \right) - 2} \right] = 0](/images/jlatex/02a23653e316404f0ca219db677627d3.gif) .
.
Apenas uma das opções seguintes pode representar a função  .
.

Nota - Em cada uma das opções estão representadas parte do gráfico de uma função e, a tracejado, uma assíntota desse gráfico.
Elabore uma composição na qual:
- identifique a opção que pode representar a função
 ;
;
- apresente as razões para rejeitar as restantes opções.
Apresente três razões diferentes, uma por cada gráfico rejeitado.
Resolução do exercício de matemática:
A tabela de monotonia da função  é a seguinte:
é a seguinte:

A opção que pode representar a função  é a IV.
é a IV.
Rejeita-se a opção I, uma vez que nesta representação gráfica a derivada no ponto de abcissa -1 é negativa e deveria ser 0.
Rejeita-se a opçãoI I, uma vez que nesta representação gráfica existe um máximo relativo para  e deveria ser um mínimo relativo, de acordo com a tabela anterior.
e deveria ser um mínimo relativo, de acordo com a tabela anterior.
Rejeita-se a opção III, uma vez que ![\mathop {\lim }\limits_{x \to + \infty } \left[ {g\left( x \right) - 2} \right] = 0 \Leftrightarrow \mathop {\lim }\limits_{x \to + \infty } g\left( x \right) = 2 \mathop {\lim }\limits_{x \to + \infty } \left[ {g\left( x \right) - 2} \right] = 0 \Leftrightarrow \mathop {\lim }\limits_{x \to + \infty } g\left( x \right) = 2](/images/jlatex/187c3a7059ba307c6f54ab5a8a78c7ed.gif) , isto é, a reta de equação
, isto é, a reta de equação 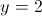 é assíntota horizontal do gráfico de
é assíntota horizontal do gráfico de  .
.
 é a seguinte:
é a seguinte:
 é a IV.
é a IV. e deveria ser um mínimo relativo, de acordo com a tabela anterior.
e deveria ser um mínimo relativo, de acordo com a tabela anterior.![\mathop {\lim }\limits_{x \to + \infty } \left[ {g\left( x \right) - 2} \right] = 0 \Leftrightarrow \mathop {\lim }\limits_{x \to + \infty } g\left( x \right) = 2 \mathop {\lim }\limits_{x \to + \infty } \left[ {g\left( x \right) - 2} \right] = 0 \Leftrightarrow \mathop {\lim }\limits_{x \to + \infty } g\left( x \right) = 2](/images/jlatex/187c3a7059ba307c6f54ab5a8a78c7ed.gif) , isto é, a reta de equação
, isto é, a reta de equação 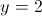 é assíntota horizontal do gráfico de
é assíntota horizontal do gráfico de  .
.
 , parte do gráfico de uma função polinomial
, parte do gráfico de uma função polinomial  , de grau 3.
, de grau 3.
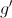 a primeira derivada de uma certa função
a primeira derivada de uma certa função  e é definida por
e é definida por  ;
;![\mathop {\lim }\limits_{x \to + \infty } \left[ {g\left( x \right) - 2} \right] = 0 \mathop {\lim }\limits_{x \to + \infty } \left[ {g\left( x \right) - 2} \right] = 0](/images/jlatex/02a23653e316404f0ca219db677627d3.gif) .
.

