Atividades Educativas

Atividades Para Imprimir

Exercícios de Matemática

Jogos de Matematica

Exames de Matemática

Exercicios de Matematica 12 ANO - Probabilidades - Exercício 15

Numa conferência de imprensa, estiveram presentes 20 jornalistas.

15.1. Considere a experiência aleatória que consiste em escolher, ao acaso, um dos 20 jornalistas presentes nessa

conferência de imprensa.

Seja X a variável aleatória «número de jornalistas do sexo feminino escolhidos».

A tabela de distribuição de probabilidades da variável X é a seguinte:

2013-f2-g2-ex3

Considere agora a experiência aleatória que consiste em escolher, ao acaso, dois dos 20 jornalistas presentes nessa

conferência de imprensa.

Seja Y a variável aleatória «número de jornalistas do sexo feminino escolhidos».

Construa a tabela de distribuição de probabilidades da variável Y.

Apresente as probabilidades na forma de fração.

15.2. Considere o problema seguinte.

«Admita que a conferência de imprensa se realiza numa sala, cujas cadeiras se encontram dispostas em cinco filas,

cada uma com oito cadeiras. Todos os jornalistas se sentam, não mais do que um em cada cadeira, nas três

primeiras filas.

De quantas maneiras diferentes se podem sentar os 20 jornalistas, sabendo que as duas primeiras filas devem

ficar totalmente ocupadas?»

Apresentam-se, em seguida, duas respostas corretas.

Resposta I) ${}^{20}{C_{16}} \times 16! \times {}^8{A_4}$ Resposta II) ${}^{20}{A_8} \times {}^{12}{A_8} \times {}^8{A_4}$

Numa composição, apresente os raciocínios que conduzem a cada uma dessas respostas.

Resolução do exercício de matemática:

15.1. A probabilidade de esolher, ao acaso, um jornalista e ele ser do sexo feminino é $\frac{3}{5}$ .

Logo, o número de jornalistas do sexo feminino é igual a $\frac{3}{5} \times 20 = 12$ .

Logo, o número de jornalistas do sexo masculino é igual a 8.

$P\left( {Y = 0} \right) = \frac{{{}^8{C_2}}}{{{}^{20}{C_2}}} = \frac{{28}}{{190}} = \frac{{14}}{{95}}$

$P\left( {Y = 1} \right) = \frac{{{}^8{C_1} \times {}^{12}{C_1}}}{{{}^{20}{C_2}}} = \frac{{96}}{{190}} = \frac{{48}}{{95}}$

$P\left( {Y = 2} \right) = \frac{{{}^{12}{C_2}}}{{{}^{20}{C_2}}} = \frac{{66}}{{190}} = \frac{{33}}{{95}}$

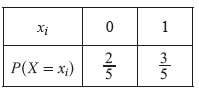
A tabela de distribuição de probabilidades da variável aleatória Y é:

2013-f2-g2-ex31

15.2. Resposta I)

Existem ${}^{20}{C_{16}}$ maneiras diferentes de formar grupos de 16 jornalistas, de entre os 20, para ocuparem as duas

primeiras filas. Para cada grupo de 16 jornalistas existem 16! maneiras de ocuparem os 16 lugares nas duas

primeiras filas. Os restantes 4 jornalistas vão-se distribuir pelas 8 cadeiras da terceira fila. Há ${}^8{A_4}$ maneiras

diferentes de estes 4 jornalistas se sentarem em 4 cadeiras, escolhidas de entre as 8 disponíveis.

Logo, existem 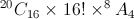${}^{20}{C_{16}} \times 16! \times {}^8{A_4}$ formas diferentes dos 20 jornalistas se sentarem.

Resposta II)

Existem ${}^{20}{A_8}$ maneiras diferentes de se sentarem, ordenadamente, 8 jornalistas escolhidos de entre os 20,

na primeira fila. Depois de sentar 8 jornalistas, restam 12. Existem ${}^{12}{A_8}$ maneiras diferentes de 8 jornalistas,

escolhidos de entre os 12, ocuparem as 8 cadeiras da segunda fila. Restam, então, 4 jornalistas para a terceira fila.

Há ${}^8{A_4}$ maneiras diferentes de estes 4 jornalistas se sentarem em 4 cadeiras, escolhidas de entre as 8 disponíveis.

Logo, existem 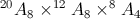${}^{20}{A_8} \times {}^{12}{A_8} \times {}^8{A_4}$ formas diferentes dos 20 jornalistas se sentarem.

Atividade de Matemática

Atividades Educativas

Atividades Para Imprimir

Exercícios de Matemática

Exames de Matemática

Jogos de Matematica

Atividades Educativas

Atividades Para Imprimir

Exercícios de Matemática

Jogos de Matematica

Exames de Matemática

Exercicios de Matematica 12 ANO - Probabilidades - Exercício 15

Atividades Relacionadas