Resolução do exercício de matemática:
• 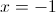
 Falso
Falso
Logo,  não é solução da inequação.
não é solução da inequação.
• 
 Verdadeiro
Verdadeiro
Logo, 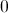 não é solução da inequação.
não é solução da inequação.
• 

 Verdadeiro
Verdadeiro
Logo,  é solução da inequação.
é solução da inequação.
Considere a inequação  .
.
Sem resolver a inequação, indique quais dos elementos do conjunto  são solução da inequação.
são solução da inequação.
• 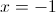
 Falso
Falso
Logo,  não é solução da inequação.
não é solução da inequação.
• 
 Verdadeiro
Verdadeiro
Logo, 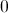 não é solução da inequação.
não é solução da inequação.
• 

 Verdadeiro
Verdadeiro
Logo,  é solução da inequação.
é solução da inequação.