1. 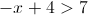
Resolução do Exercício de Inequações do 1º Grau

![S = \left] { - \infty , - 3} \right[ S = \left] { - \infty , - 3} \right[](/images/jlatex/c1456e2d159c2940c4b91e7a2227cb63.gif)
2. 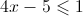
Resolução do Exercício de Inequações do 1º Grau

![S = \left] { - \infty ,\frac{3}{2}} \right] S = \left] { - \infty ,\frac{3}{2}} \right]](/images/jlatex/ba63a0881aafedd790195221971d4d97.gif)
3. 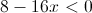
Resolução do Exercício de Inequações do 1º Grau

![S = \left] {\frac{1}{2}, + \infty } \right[ S = \left] {\frac{1}{2}, + \infty } \right[](/images/jlatex/a11cb5b2e628ac302ff16434796ef40e.gif)
4. 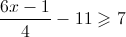
Resolução do Exercício de Inequações do 1º Grau



5. 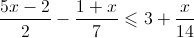
Resolução do Exercício de Inequações do 1º Grau




![S = \left] { - \infty ,2} \right] S = \left] { - \infty ,2} \right]](/images/jlatex/b528988955018311e67acfffb00e7b2d.gif)

 , cada uma das seguintes inequações e apresente a solução sob a forma de intervalos de números reais.
, cada uma das seguintes inequações e apresente a solução sob a forma de intervalos de números reais.