Resolução do exercício de matemática:
3.1.


3.2. O declive da reta tangente ao gráfico da função  no ponto de abcissa
no ponto de abcissa  é igual a
é igual a  .
.



Logo, o declive da reta tangente ao gráfico da função  no ponto de abcissa
no ponto de abcissa  é igual a
é igual a  .
.

 , o triângulo [OAB] e a reta
, o triângulo [OAB] e a reta 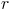 .
.

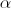 , por
, por  .
.
