Exercicios de Matematica 12 ANO - Função exponencial e logarítmica - Exercício 2

Considere a função , de domínio $\mathbb{R}$ , definida por:

2014-f1-g2-ex5

Resolva os itens seguintes, recorrendo a métodos analíticos, sem utilizar a calculadora.

5.1. Averigue se a função é contínua em x = 4 .

5.2. O gráfico da função tem uma assíntota oblíqua quando 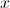tende para $+ \infty$ , de equação y = x + b , com $b \in \mathbb{R}$ .

Determine .

Resolução do exercício de matemática:

5.1.

$\mathop {\lim }\limits_{x \to {4^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {4^ - }} \frac{{{e^{x - 4}} - 3x + 11}}{{4 - x}} = \mathop {\lim }\limits_{y \to {0^ - }} \frac{{{e^y} - 3\left( {y + 4} \right) + 11}}{{ - y}} =$

$= - \mathop {\lim }\limits_{y \to {0^ - }} \frac{{{e^y} - 3y - 12 + 11}}{y} = - \mathop {\lim }\limits_{y \to {0^ - }} \frac{{{e^y} - 3y - 1}}{y} = - \mathop {\lim }\limits_{y \to {0^ - }} \left( {\frac{{{e^y} - 1}}{y} - \frac{{3y}}{y}} \right) =$

$= - \mathop {\lim }\limits_{y \to {0^ - }} \left( {\frac{{{e^y} - 1}}{y} - 3} \right) = - \mathop {\lim }\limits_{y \to {0^ - }} \frac{{{e^y} - 1}}{y} + 3 = - 1 + 3 = 2$

(Mudança de variável: y = x - 4 (quando $x \to {4^ - }$ , $y \to {0^ - }$ )).

$\mathop {\lim }\limits_{x \to {4^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {4^ + }} \left( {\ln \left( {2{e^x} - {e^4}} \right)} \right) = \ln \left( {2{e^4} - {e^4}} \right) = \ln \left( {{e^4}} \right) = 4$

Como $\mathop {\lim }\limits_{x \to {4^ - }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {4^ + }} f\left( x \right)$ , não é contínua em x = 4 .

5.2.

$b = \mathop {\lim }\limits_{x \to + \infty } \left( {f\left( x \right) - x} \right) = \mathop {\lim }\limits_{x \to + \infty } \left( {\ln \left( {2{e^x} - {e^4}} \right) - x} \right) = \mathop {\lim }\limits_{x \to + \infty } \left( {\ln \left( {2{e^x} - {e^4}} \right) - \ln {e^x}} \right) =$

$= \mathop {\lim }\limits_{x \to + \infty } \left( {\ln \left( {\frac{{2{e^x} - {e^4}}}{{{e^x}}}} \right)} \right) = \mathop {\lim }\limits_{x \to + \infty } \left( {\ln \left( {\frac{{2{e^x}}}{{{e^x}}} - \frac{{{e^4}}}{{{e^x}}}} \right)} \right) = \mathop {\lim }\limits_{x \to + \infty } \left( {\ln \left( {2 - \frac{{{e^4}}}{{{e^x}}}} \right)} \right) =$