
Almada Negreiros, escritor e artista plástico, concebeu, no final da década de 1950, um conjunto de quadros de natureza abstracta, nos quais a Geometria e o Número são o tema central.
A Figura 3 apresenta uma fotografia de um desses quadros,
A Porta da Harmonia, um óleo sobre tela, pintado a preto e branco.
A Figura 4, que não está à escala, mostra uma composição geométrica representativa do quadro, constituída pelos quadrados [OPQR], [ABCD], [EFGH] e [IFJL] e posicionada no primeiro quadrante de um referencial ortogonal e monométrico  .
.
Os lados [OP] e [OR] do quadrado [OPQR] estão contidos,
respetivamente, no semieixo positivo 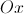 e no semieixo
e no semieixo
positivo 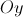 desse referencial.
desse referencial.
Considere que:
• [ABCD] está inscrito em [OPQR]
• o ponto B tem coordenadas (14 , 6)
• o ponto A tem abcissa 6
• os vértices de [EFGH] são os pontos médios
dos lados de [ABCD]
• [IFJL] está contido em [ABCD]
• a razão de semelhança entre [EFGH] e [IFJL]
é 
• o ponto M é o ponto de interseção de [EF]
com [IL]
1. Mostre que  .
.
2. Mostre que o comprimento do lado do quadrado [IFJL] é exatamente metade do comprimento do lado do quadrado [ABCD].
Sugestão – Na sua resposta, poderá começar por calcular o comprimento do lado do quadrado [EFGH] e utilizar a razão de semelhança entre os quadrados [EFGH] e [IFJL] para calcular o comprimento do lado do quadrado [IFJL].
3. Admita que o quadrado [IFJL] pode rodar em torno do ponto F, de modo a  tomar valores entre 0 e 5, e que, nesse movimento, o triângulo [IFM] se mantém não sombreado.
tomar valores entre 0 e 5, e que, nesse movimento, o triângulo [IFM] se mantém não sombreado.
Considere  .
.
Seja a função real de variável real definida por
 com
com 
Para cada valor de 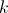 , a função
, a função  permite obter a área da parte da composição representada a sombreado.
permite obter a área da parte da composição representada a sombreado.
Existe algum valor de 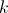 para o qual a área da parte da composição representada a sombreado corresponda a 40% da área do quadrado [OPQR]?
para o qual a área da parte da composição representada a sombreado corresponda a 40% da área do quadrado [OPQR]?
Justifique a sua resposta.
Resolução do exercício de matemática:
1.




Logo,  .
.
2.


Como a razão de semelhança entre os quadrados [EFGH] e [IFJL] é  , tem-se que:
, tem-se que:

Logo,  .
.
Logo, o comprimento do lado do quadrado [IFJL] é metade do comprimento do lado do quadrado [ABCD].
3.
A área do quadrado [OPQR] é igual a 14x14=196.
desta área é igual a 0,4x196=78,4.

impossível , uma vez que  .
.
Logo, não existe nenhum valor de para o qual a área da parte da composição representada a sombreado corresponda a 40% da área do quadrado [OPQR].




 .
.

 , tem-se que:
, tem-se que:
 .
.
 .
.

 .
.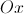 e no semieixo
e no semieixo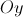 desse referencial.
desse referencial. tomar valores entre 0 e 5, e que, nesse movimento, o triângulo [IFM] se mantém não sombreado.
tomar valores entre 0 e 5, e que, nesse movimento, o triângulo [IFM] se mantém não sombreado. .
. com
com 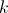 , a função
, a função  permite obter a área da parte da composição representada a sombreado.
permite obter a área da parte da composição representada a sombreado.