A Jalur é uma empresa que produz, artesanalmente, janelas de estilo antigo para o mercado de uma certa região. O gestor da Jalur sabe que a empresa consegue vender, nesse mercado, todas as janelas que produzir.
As janelas de estilo antigo produzidas pela Jalur são de dois tipos: Tipo I e Tipo II.
Sabe-se que:
- para produzir uma janela do Tipo I, são necessárias uma hora na secção de corte, três horas na secção de polimento e duas horas na secção de acabamentos;
- para produzir uma janela do Tipo II, são necessárias uma hora na secção de corte, duas horas na secção de polimento e uma hora na secção de acabamentos;
- as secções de produção da Jalur têm, semanalmente, a seguinte disponibilidade:
• secção de corte: 16 horas;
• secção de polimento: 36 horas;
• secção de acabamentos: 22 horas.
O lucro que a Jalur obtém ao vender uma janela do Tipo I é 30 euros, e o que obtém ao vender uma janela do Tipo II é 25 euros.
Designe por o número de janelas do Tipo I produzidas, semanalmente, pela Jalur, e designe por 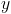 o número de janelas do Tipo II produzidas, semanalmente, pela Jalur.
o número de janelas do Tipo II produzidas, semanalmente, pela Jalur.
1. É possível a Jalur produzir um total de 15 janelas de estilo antigo, numa semana?
Justifique a sua resposta.
2. Determine, quantas janelas do Tipo I e quantas janelas do Tipo II deve a Jalur produzir, semanalmente, para, nas condições referidas, obter lucro máximo.
Na sua resposta, percorra, sucessivamente, as seguintes etapas:
• indicar a função objetivo;
• indicar as restrições do problema;
• representar, graficamente, a região admissível referente ao sistema de restrições;
• calcular o número de janelas do Tipo I e o número de janelas do Tipo II que a Jalur deve produzir, semanalmente, correspondentes à solução do problema.
Resolução do exercício de matemática:
1.
É possível a Jalur produzir um total de 15 janelas de estilo antigo.
Se as 15 janelas forem do Tipo II, serão ocupadas:
• 15 horas na secção de corte (15 < 16);
• 30 horas na secção de polimento (30 < 36);
• 15 horas na secção de acabamentos (15 < 22).
2.
• função objetivo: 
• restrições do problema:

• região admissível:












• Deve produzir 4 janelas do Tipo I e 12 janelas do Tipo II para ter lucro máximo (420 Eur.).















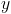 o número de janelas do Tipo II produzidas, semanalmente, pela Jalur.
o número de janelas do Tipo II produzidas, semanalmente, pela Jalur.