Resolução dos Exercícios de Matemática de Sistema de Equações:
1.



Sistema possível e determinado Solução: 
2.



Sistema possível e indeterminado. As soluções do sistema são os pontos de coordenadas 
3.


Sistema impossível 
Resolva e classifique os seguintes sistemas:
1.
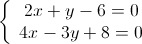
2.
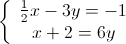
3.
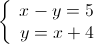
Resolução dos Exercícios de Matemática de Sistema de Equações:
1.



Sistema possível e determinado Solução: 
2.



Sistema possível e indeterminado. As soluções do sistema são os pontos de coordenadas 
3.


Sistema impossível 