Resolução do Exercício de Matemática:
1.


Sistema impossível 
2.



Sistema possível e determinado 
3.



Sistema possível e indeterminado 
Resolva e classifique cada um dos sistemas.
1.
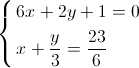
2.
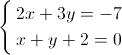
3.
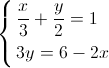
Resolução do Exercício de Matemática:
1.


Sistema impossível 
2.



Sistema possível e determinado 
3.



Sistema possível e indeterminado 