Trigonometria no Triângulo Retângulo - Exercício 1 - Geometria

Trigonometria no Triângulo Retângulo

A figura mostra uma sala com 3 metros de altura. O chão é retangular e o comprimento deste excede a largura em 2 metros.

exercicio-1

Sendo $\small x$ a largura da sala, escreva, em função de $\small x$ uma expressão que represente:

(a) a área do chão;

(b) a área da cada parede

Se se gastaram $\small 107m^{2}$ de papel para forrar as paredes e o teto, quanto dinheiro se vai gastar para colocar madeira no chão ao preço de R$466 o metro quadrado da madeira?

Resolução do exercício de matemática:

1. (a)

Se a largura da sala mede $\small x$ metros então o comprimento da sala será $\small x+2$ metros.

A área retangular da sala é dada por comprimento X largura, sendo a função que represente a área do chão da sala temos,

$A(x)= x\times (x+2) \Leftrightarrow A(x)= x^{2}+2x$

1. (b)

O comprimento das paredes maiores é dada por $\small x+2$ metros, o comprimento das paredes menores é dada por $\small x$ metros e a altura de cada parede é de 3 metros.

A área retangular das paredes maiores é dada por comprimento X largura, sendo a função que represente a área dessas paredes da sala temos,

$B(x)= 3\times (x+2) \Leftrightarrow B(x)= 3x+6$

A área retangular das paredes menores é dada por comprimento X largura, sendo 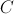a função que represente a área dessas paredes da sala temos,

C(x)= 3 x

Para resolver este exercício teremos de calcular o valor de $\small x$ que representa a largura da sala.

Se se gastaram $\small 107m^{2}$ de papel para forrar as paredes e o teto,

então, pelo item 1, temos que a área das paredes é $2\times B(x) + 2\times C(x)$ ,

como a área do chão é igual á área do teto vem que,

$2\times B(x) + 2\times C(x) + A(x) = 107m^{2} \Leftrightarrow$

$\Leftrightarrow 2\times (3x+6) + 2\times (3x) + x^{2}+2x = 107 \Leftrightarrow$

$\Leftrightarrow x^{2}+2x +6x +12 +6x - 107 = 0 \Leftrightarrow$

$\Leftrightarrow x^{2}+14x -95= 0 \Leftrightarrow x = \frac{{ - 14 \pm \sqrt {{{14}^2} + 380} }}{2}$

$\Leftrightarrow x = \frac{{ - 14 \pm \sqrt {576} }}{2} \Leftrightarrow x = \frac{{ - 14 + 24}}{2} \vee x = \frac{{ - 14 - 24}}{2}$ -> Valor impossível, a área é sempre um valor positivo $\Rightarrow$