Trigonometria no Triângulo Retângulo - Exercício 2 - Geometria

Trigonometria no Triângulo Retângulo

Na figura, [ABC] é um triângulo isósceles e [CM] a altura relativa à base [AB]. De acordo com os dados da figura determine:

1. O valor de .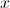

2. $\overline {AC}$ .

3. A área do triângulo [ABC].

(As medidas são em metros.)

exercicio-2

Resolução do exercício de matemática:

Como o triângulo é isósceles e [CM] é a altura relativa à base [AB], então:

$\overline {CM} = \frac{{\overline {AB} }}{2} \Leftrightarrow \overline {CM} = \frac{{2x + 4}}{2} \Leftrightarrow \overline {CM} = x + 2$

Pelo teorema de Pitágoras temos que:

${\overline {CB} ^2} = {\overline {CM} ^2} + {\overline {MB} ^2}$

Logo,

$\begin{gathered} {\left( {x + 6} \right)^2} = {\left( {x + 2} \right)^2} + {\left( {2x} \right)^2} \Leftrightarrow {x^2} + 12x + 36 = {x^2} + 4x + 4 + 4{x^2} \Leftrightarrow \hfill \\ \Leftrightarrow - 4{x^2} + 8x + 32 = 0 \Leftrightarrow {x^2} - 2x - 8 = 0 \Leftrightarrow \hfill \\ \Leftrightarrow x = \frac{{2 \pm \sqrt {{{\left( { - 2} \right)}^2} - 4 \times 1 \times ( - 8)} }}{2} \Leftrightarrow x = \frac{{2 \pm \sqrt {36} }}{2} \Leftrightarrow \hfill \\ \Leftrightarrow x = \frac{{2 + 6}}{2} \vee x = \frac{{2 - 6}}{2} \Leftrightarrow \hfill \\ \Leftrightarrow x = 4 \vee x = - 2{\text{ }} \to {\text{ Imposs\'i vel o comprimento \'e sempre positivo}} \hfill \\ \end{gathered}$