Exame Nacional de Matemática B 2ª Fase 2011 - Grupo 1 - Exercício 1

Durante séculos, os moínhos de vento serviram para moer trigo e obter a farinha com que se fabricava o pão.

A Figura 1 apresenta a fotografia de um moínho de vento, de tipo mediterrânico.

O moínho é posto a funcionar pela ação do vento, que faz rodar as suas velas, fixadas e esticadas num conjunto de 8 varas.

Admita que as varas têm todas o mesmo comprimento e que se unem no mesmo ponto.

As figuras 2 e 3 representam, esquematicamente, duas posições distintas das velas de um mesmo moínho.

O esquema representado em cada uma das figuras tem a forma de um octógono regular, e os pontos O e V assinalam as extremidades de uma das varas.

 Admita que:

• num certo dia, as velas rodaram, no sentido indicado na Figura 3, durante um quarto de hora, com velocidade constante;

• no instante inicial, a vara representada por estava posicionada paralelamente ao solo, como sugere a Figura 2;

• a distância, , em metros, do ponto ao solo, 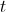segundos após as velas terem começado a rodar, é dada, durante o intervalo de tempo em que as velas rodaram, por

para

O argumento da função co-seno está em radianos.

1. Determine o comprimento de uma vara.

Sugestão:

Na sua resposta, poderá começar por apresentar o gráfico da função num intervalo
adequado, por exemplo , e assinalar os pontos relevantes para a resolução do
problema.