Resolução do Exercício:
1.
Rotação de centro O e amplitude  .
.
2.
Pelo Teorema de Pitágoras, tem-se que:


Logo,  .
.
Logo o ponto simétrico de  em relação ao eixo das ordenadas (ponto
em relação ao eixo das ordenadas (ponto 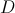 ) tem coordenadas
) tem coordenadas  .
.
Na Figura 4 estão representados o octógono regular ![\left[ {ABCDEFGH} \right] \left[ {ABCDEFGH} \right]](/images/jlatex/6c587cd222f453012dfd43a1171f5cd7.gif) , com centro no ponto
, com centro no ponto  , os segmentos de reta
, os segmentos de reta ![\left[ {FB} \right] \left[ {FB} \right]](/images/jlatex/4d2a6c7fbf05a9613b06ca886da6776a.gif) e
e ![\left[ {DH} \right] \left[ {DH} \right]](/images/jlatex/36c233ebd45dc8eb11755cd7c9ed1fef.gif) e as retas
e as retas  e
e  .
.

1. Uma rotação é uma transformação geométrica que é caracterizada pelo seu centro e por uma amplitude do ângulo de rotação.
Caracterize uma rotação que transforme o ponto  no ponto
no ponto  .
.
2. Considere o referencial ortogonal e monométrico, com origem no ponto  , no qual os pontos
, no qual os pontos  e
e 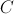 pertencem, respetivamente, aos semieixos positivos das abcissas e das ordenadas, tendo o ponto
pertencem, respetivamente, aos semieixos positivos das abcissas e das ordenadas, tendo o ponto  coordenadas
coordenadas  .
.
Determine as coordenadas do ponto simétrico de  relativamente ao eixo das ordenadas.
relativamente ao eixo das ordenadas.
Resolução do Exercício:
1.
Rotação de centro O e amplitude  .
.
2.
Pelo Teorema de Pitágoras, tem-se que:


Logo,  .
.
Logo o ponto simétrico de  em relação ao eixo das ordenadas (ponto
em relação ao eixo das ordenadas (ponto 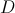 ) tem coordenadas
) tem coordenadas  .
.