Exame Nacional de Matemática B 2ª Fase 2011 - Grupo 2

exame 2011 2f g2 ex1

A Figura 5 representa uma gravura intitulada Divisão Regular de Superfície, de autoria de M. C. Escher.

A Figura 6 representa uma versão simplificada de parte do diagrama de suporte usado por Escher na elaboração da gravura, na qual se observam várias linhas de quadrados .

A partir de um segmento de reta $\left[ {AB} \right]$ , constroem-se dois quadrados geometricamente iguais, $\left[ {ACED} \right]$ e $\left[ {CBFE} \right]$ , obtendo-se a linha 1 de quadrados.

Repete-se o processo, sucessivamente, de modo a obter novas linhas de quadrados, como sugere a Figura 6.

Admita que:
• $\overline {AB} = 8{\text{ dm}}$
• a linha 1 é constituída por 2 quadrados com 4 dm de lado;
• a linha 2 é constituída por 4 quadrados com 2 dm de lado;
• de cada linha para a linha seguinte, o número de quadrados duplica e o comprimento do lado de cada quadrado diminui para metade.

Admita, também, que se podem obter tantas linhas de quadrados quantas se queira.

Considere a sucessão $\left( {{a_n}} \right)$ , cujo termo de ordem 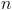dá a área total, em dm2, dos quadrados que constituem a linha 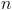. Nesta sucessão, o primeiro termo, que corresponde à área total dos quadrados da linha 1, é 32 e o segundo termo, que corresponde à área total dos quadrados da linha 2, é 16.

1. Mostre que a área ocupada por todos os quadrados das primeiras 7 linhas é exatamente 63,5 dm2.

2. Sempre que se acrescenta uma nova linha de quadrados, a soma das áreas de todos os quadrados, incluindo os dessa linha, aumenta.

Resulução do exercício de matemática:

$\left( {{a_n}} \right)$ é uma progressão geométrica de razão $\frac{1}{2}$ e primeiro termo 32 dm2.
${S_7} = \frac{{1 - {{\left( {\frac{1}{2}} \right)}^7}}}{{1 - \frac{1}{2}}} \times 32 = \frac{{1 - \frac{1}{{128}}}}{{\frac{1}{2}}} \times 32 = \frac{{\frac{{127}}{{128}}}}{{\frac{1}{2}}} \times 32 = \frac{{127}}{{64}} \times 32 = 63,5$

A área pedida é de 63,5 dm2.

${S_n} = 64 \Leftrightarrow \frac{{1 - {{\left( {\frac{1}{2}} \right)}^n}}}{{1 - \frac{1}{2}}} \times 32 = 64 \Leftrightarrow \frac{{1 - {{\left( {\frac{1}{2}} \right)}^n}}}{{\frac{1}{2}}} = 2 \Leftrightarrow$

$\Leftrightarrow 1 - {\left( {\frac{1}{2}} \right)^n} = 1 \Leftrightarrow {\left( {\frac{1}{2}} \right)^n} = 0$

Esta igualdade é impossível uma vez que ${\left( {\frac{1}{2}} \right)^n} > 0,\forall n \in \mathbb{N}$ .

Logo, a soma das áreas não pode ser igual a 64 dm2.

Atividade de Matemática

Atividades Educativas

Atividades Para Imprimir

Exercícios de Matemática

Exames de Matemática

Jogos de Matematica