Resolva, em , cada uma das seguintes inequações e apresente a solução sob a forma de intervalos de números reais.

1.

2.

3.

4.

5.

Exercícios de Matemática 9º ano - Geometria no Plano e no Espaço - Exercício 2

Determine 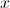em cada uma das figuras seguintes.

1.        2.

Considere a função , de domínio , e a função , de domínio , definidas por:

e

1. Mostre que é o único zero da função , recorrendo a métodos
exclusivamente analíticos.

2. Considere, num referencial o.n. , os gráficos das funções e e o triângulo .

Sabe-se que:

• é a origem do referencial;

• e são pontos do gráfico de ;

• a abcissa do ponto é o zero da função ;

• o ponto é o ponto de interseção do gráfico da função com o gráfico da função .

Determine a área do triângulo , recorrendo à calculadora gráfica.

Na sua resposta, deve:

• reproduzir os gráficos das funções e , devidamente identificado(s), incluindo o referencial;

• assinalar os pontos e ;

• indicar a abcissa do ponto e as coordenadas do ponto com arredondamento às centésimas;

• apresentar o valor da área pedida com arredondamento às décimas.

Numa escola, realizou-se um estudo sobre os hábitos alimentares dos alunos. No âmbito desse estudo, analisou-se o peso de todos os alunos.
Sabe-se que:

• 55% dos alunos são raparigas;

• 30% das raparigas têm excesso de peso;

• 40% dos rapazes não têm excesso de peso;

1. Escolhe-se, ao acaso, um aluno dessa escola.

Determine a probabilidade de o aluno escolhido ser rapaz, sabendo que tem excesso de peso.

Apresente o resultado na forma de fração irredutível.

2. Considere agora que a escola onde o estudo foi realizado tem 200 alunos.

Pretende-se escolher, ao acaso, três alunos para representarem a escola num concurso.

Determine a probabilidade de serem escolhidos duas raparigas e um rapaz.

Apresente o resultado com arredondamento às centésimas.

Num saco estão cinco bolas, indistinguíveis ao tato, cada uma delas numerada com um número diferente: -2, -1, 0, 1 e 2.

Extraem-se, ao acaso e em simultâneo, quatro bolas do saco.

Seja X a variável aleatória «produto dos números inscritos nas bolas extraídas».

A tabela de distribuição de probabilidades da variável X é a seguinte.

Elabore uma composição na qual:

• explique os valores da variável X

• justifique cada uma das probabilidades.

Atividades de Matemática para Educação Infantil - Soma de Conjuntos

Problemas de Soma de Conjuntos para imprimir da 1ª Série.

2. Para assistirem a um espetáculo, o João, a Margarida e cinco amigos sentam-se, ao acaso, numa fila com sete lugares.

Qual é a probabilidade de o João e a Margarida não ficarem sentados um ao lado do outro?

(A)

(B)

(C)

(D)

Seja 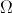o espaço de resultados associado a uma certa experiência aleatória, e sejam e dois acontecimentos .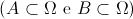

Sabe-se que:

• e são acontecimentos independentes;

•

•

Qual é o valor de ?

(A)

(B)

(C)

(D)