Considere a função , de domínio
, de domínio , definida por
, definida por .
.
1.
O gráfico de admite uma assíntota horizontal.
de admite uma assíntota horizontal.
Seja o ponto de interseção dessa assíntota com a reta tangente ao gráfico
o ponto de interseção dessa assíntota com a reta tangente ao gráfico de no ponto de abcissa
de no ponto de abcissa .
.
Determine as coordenadas do ponto recorrendo a métodos exclusivamente analíticos.
recorrendo a métodos exclusivamente analíticos.
2.
Existem dois pontos do gráfico de cujas ordenadas são o cubo das abcissas.
Determine as coordenadas desses pontos recorrendo à calculadora gráfica.
Na sua resposta, deve:
- equacionar o problema;
- reproduzir o gráfico da função ou os gráficos das funções que tiver necessidade de visualizar na calculadora, devidamente identificado(s), incluindo o referencial;
- assinalar esses pontos;
- indicar as coordenadas desses pontos com arredondamento às centésimas.
Exame Nacional de Matemática 12º Ano 1ª Fase 2011 - Grupo 2 - Exercício 5→
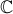 o conjunto dos números complexos.
o conjunto dos números complexos. e
e  , com
, com  e
e  .
. para o qual
para o qual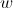 é um número real.
é um número real. um número complexo tal que
um número complexo tal que  .
. .
.
 é a imagem geométrica do número complexo
é a imagem geométrica do número complexo 
 tem abcissa negativa, ordenada nula, e pertence À circunferência de centro na origem do referencial e raio igual a
tem abcissa negativa, ordenada nula, e pertence À circunferência de centro na origem do referencial e raio igual a 

 a determinação que pertence ao intervalo
a determinação que pertence ao intervalo  )
)



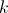 , a função
, a função  definida em
definida em  por:
por:
![\sqrt[3]{e} \sqrt[3]{e}](/images/jlatex/fbf1ec86e8fd79251b9fa5725d7b74d7.gif)



 um número real positivo e seja X uma variável aleatória com distribuição Normal
um número real positivo e seja X uma variável aleatória com distribuição Normal  .
.








 , de domínio
, de domínio .
. o ponto de interseção dessa assíntota com a reta tangente ao gráfico
o ponto de interseção dessa assíntota com a reta tangente ao gráfico .
.