Exame Nacional de Matemática B 1ª Fase 2011 - Grupo 1 - Exercício 2
Na edição de 2010 da feira anual, a organização do jogo Roda da Fortuna limitou o número total de inscrições no jogo. Estipulou que, em cada dia de feira, haveria, no máximo, mais 8 inscrições do que no dia anterior.
No final da feira desse ano, a organização revelou que, no primeiro dia, houve 6 inscrições no jogo Roda da Fortuna e que, nos restantes dias, se esgotou o número de inscrições estipulado para cada um dos dias.
1. Determine o número de inscrições feitas no décimo dia da feira anual de 2010.
2. Admita que, nos dois últimos dias da feira anual de 2010, houve um total de 340 inscrições na Roda da Fortuna.
Determine o número de dias que durou a feira anual de 2010.
Exame Nacional de Matemática B 1ª Fase 2011 - Grupo 1 - Exercício 2→

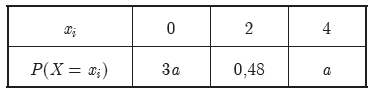
 representa um número real.
representa um número real.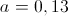 .
. , o conjunto solução de cada uma das seguintes condições:
, o conjunto solução de cada uma das seguintes condições:



 , definida em
, definida em  .
.
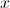 .
. .
.

 a largura da sala, escreva, em função de
a largura da sala, escreva, em função de de papel para forrar as paredes e o teto, quanto dinheiro se vai gastar para colocar madeira no chão ao preço de R$466 o metro quadrado da madeira?
de papel para forrar as paredes e o teto, quanto dinheiro se vai gastar para colocar madeira no chão ao preço de R$466 o metro quadrado da madeira? Resposta II:
Resposta II: 