Uma companhia aérea vende bilhetes a baixo custo exclusivamente para viagens cujos destinos sejam Berlim ou Paris.
1.
Nove jovens decidem ir a Berlim e escolhem essa companhia aérea. Cada jovem paga o bilhete com cartão multibanco, ou não, independentemente da forma de pagamento utilizado pelos outros jovens.
Considere que a probabilidade de um jovem utilizar cartão multibanco, para pagar o seu bilhete, é igual a 0,6.
Determine a probabilidade de exatamente 6 desses jovens utilizarem cartão multibanco para pagarem o seu bilhete.
Apresente o resultado com arredondamento às centésimas.
2.
A companhia aérea constatou que, quando o destino é Berlim, 5% dos seus passageiros perdem o voo e que, quando o destino é Paris , 92% dos passageiros seguem viagem. Sabe-se que 30% dos bilhetes a baixo custo que a companhia vende têm por destino Berlim.
Determine a probabilidade de um passageiro, que comprou bilhete a baixo custo nessa companhia aérea, perder o voo.
Apresente o resultado na forma de dízima.
Exame Nacional de Matemática 12º Ano 1ª Fase 2011 - Grupo 2 - Exercício 2→
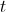 horas após as zero horas do dia 1 de Abril de 2010, é dada, aproximadamente, por
horas após as zero horas do dia 1 de Abril de 2010, é dada, aproximadamente, por , com
, com![t \in \left[ {0,20} \right] t \in \left[ {0,20} \right]](/images/jlatex/ebd251221fca80cf7138e1bd16eb7ca2.gif)

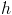 definida por
definida por 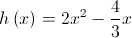 .
.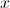 de tais que
de tais que 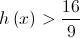 .
. , parte do gráfico da função
, parte do gráfico da função  .
.

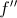 , de uma certa função
, de uma certa função  tem domínio
tem domínio 


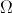 o espaço de resultados associado a uma certa experiência aleatória, e sejam
o espaço de resultados associado a uma certa experiência aleatória, e sejam e
e dois acontecimentos
dois acontecimentos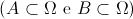 , com
, com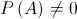 .
. .
.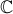 , conjunto dos números complexos, considere
, conjunto dos números complexos, considere ,
, e
e
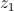 é raiz do polinómio
é raiz do polinómio .
.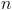 natural para o qual a imagem geométrica de
natural para o qual a imagem geométrica de , no plano complexo, está no terceiro quadrante e pertence à bissetriz dos quadrantes ímpares.
, no plano complexo, está no terceiro quadrante e pertence à bissetriz dos quadrantes ímpares.![\left[ {AB} \right] \left[ {AB} \right]](/images/jlatex/103109231bf469cee07093a66be902fa.gif) é um dos lados de um polígono regular cujos vértices são as imagens geométricas das raízes de índice 5 do complexo
é um dos lados de um polígono regular cujos vértices são as imagens geométricas das raízes de índice 5 do complexo ;
; está contido na circunferência de centro na origem do referencial e raio igual a
está contido na circunferência de centro na origem do referencial e raio igual a .
.
 ?
?



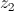 ,
, e
e .
.
 , pode ser igual a
, pode ser igual a ?
?