A empresa AP comercializa pacotes de açúcar.
1. Seja Y a variável aleatória «massa, em gramas, de um pacote de açúcar comercializado pela empresa AP».
A variável aleatória Y segue uma distribuição normal de valor médio 6,5 gramas e desvio padrão 0,4 gramas.
Um pacote de açúcar encontra-se em condições de ser comercializado se a sua massa estiver compreendida entre 5,7 gramas e 7,3 gramas.
Determine o valor aproximado da probabilidade de, em 10 desses pacotes de açúcar, exatamente oito estarem em condições de ser comercializados.
Apresente o resultado na forma de dízima, com aproximação às milésimas.
2. Considere o problema seguinte.
«A empresa AP pretende aplicar, junto dos seus funcionários, um programa de reeducação alimentar.
De entre os 500 funcionários da empresa AP vão ser selecionados 30 para formarem um grupo para
frequentar esse programa.
A Joana e a Margarida são irmãs e são funcionárias da empresa AP.
Quantos grupos diferentes podem ser formados de modo que, pelo menos, uma das duas irmãs, a Joana ou a Margarida, não seja escolhida para esse grupo?».
Apresentam-se, em seguida, duas respostas corretas.
I) 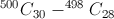 II)
II) 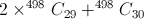
Numa composição, apresente o raciocínio que conduz a cada uma dessas respostas.
Resolução do exercício de matemática:
1.
Seja  a massa, em gramas, de um pacote de açúcar está compreendida entre 5,7 e 7,3.
a massa, em gramas, de um pacote de açúcar está compreendida entre 5,7 e 7,3.
 .
.

Seja  o número de pacotes com massa, em gramas, compreendida entre 5,7 e 7,3 em 10 pacotes.
o número de pacotes com massa, em gramas, compreendida entre 5,7 e 7,3 em 10 pacotes.

2. Na resposta I, 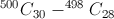 representa a diferença entre o número total de grupos de 30 funcionários que se podem formar com os 500 existentes e o número de grupos diferentes que se podem formar, nos quais a Joana e a Margarida estão presentes.
representa a diferença entre o número total de grupos de 30 funcionários que se podem formar com os 500 existentes e o número de grupos diferentes que se podem formar, nos quais a Joana e a Margarida estão presentes.
Na resposta II,  representa o número de grupos diferentes que se podem formar com apenas uma das irmãs presentes.
representa o número de grupos diferentes que se podem formar com apenas uma das irmãs presentes.  representa o número de grupos diferentes que se podem formar em que nenhuma das irmãs está presente. Logo,
representa o número de grupos diferentes que se podem formar em que nenhuma das irmãs está presente. Logo, 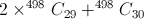 representa o número de grupos diferentes, nos quais pelo menos uma das irmãs não está presente.
representa o número de grupos diferentes, nos quais pelo menos uma das irmãs não está presente.
 a massa, em gramas, de um pacote de açúcar está compreendida entre 5,7 e 7,3.
a massa, em gramas, de um pacote de açúcar está compreendida entre 5,7 e 7,3. .
.
 o número de pacotes com massa, em gramas, compreendida entre 5,7 e 7,3 em 10 pacotes.
o número de pacotes com massa, em gramas, compreendida entre 5,7 e 7,3 em 10 pacotes.
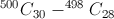 representa a diferença entre o número total de grupos de 30 funcionários que se podem formar com os 500 existentes e o número de grupos diferentes que se podem formar, nos quais a Joana e a Margarida estão presentes.
representa a diferença entre o número total de grupos de 30 funcionários que se podem formar com os 500 existentes e o número de grupos diferentes que se podem formar, nos quais a Joana e a Margarida estão presentes. representa o número de grupos diferentes que se podem formar com apenas uma das irmãs presentes.
representa o número de grupos diferentes que se podem formar com apenas uma das irmãs presentes.  representa o número de grupos diferentes que se podem formar em que nenhuma das irmãs está presente. Logo,
representa o número de grupos diferentes que se podem formar em que nenhuma das irmãs está presente. Logo, 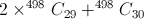 representa o número de grupos diferentes, nos quais pelo menos uma das irmãs não está presente.
representa o número de grupos diferentes, nos quais pelo menos uma das irmãs não está presente.




