Na figura 4, está representado o quadrado ![\left[ {ABCD} \right] \left[ {ABCD} \right]](/images/jlatex/7c39be72ce8fa6c0bf88b67de000cf8a.gif) .
.

Sabe-se que:

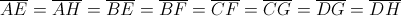
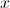 é a amplitude, em radianos, do ângulo
é a amplitude, em radianos, do ângulo 
![x \in \left] {0,\frac{\pi }{4}} \right[ x \in \left] {0,\frac{\pi }{4}} \right[](/images/jlatex/1727a76c7b24d07cc2f02c138d383154.gif)
1. Mostre que a área da região sombreada é dada, em função de 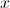 , por
, por
 .
.
2. Mostre que existe um valor de 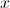 compreendido entre
compreendido entre  e
e  para o qual a área da região sombreada é 5.
para o qual a área da região sombreada é 5.
Se utilizar a calculadora em eventuais cálculos numéricos, sempre que proceder a arredondamentos, use duas casas decimais.
Resolução do exercício de matemática:
1.
Os triângulos ![\left[ {ABE} \right] \left[ {ABE} \right]](/images/jlatex/5ed4c69f7b62a9b923db1773cb12c6d7.gif) ,
, ![\left[ {BCF} \right] \left[ {BCF} \right]](/images/jlatex/f068e07053c05b6ed15028b9c167dce8.gif) ,
, ![\left[ {CDG} \right] \left[ {CDG} \right]](/images/jlatex/fe95f8a2de609f2b806a7696a89b24a3.gif) e
e ![\left[ {DAH} \right] \left[ {DAH} \right]](/images/jlatex/efe553cd8542b2725f02b7e41c5cb027.gif) são geometricamente iguais.
são geometricamente iguais.
Seja M o ponto médio de ![\left[ {AB} \right] \left[ {AB} \right]](/images/jlatex/103109231bf469cee07093a66be902fa.gif) .
.

![{A_{\vartriangle \left[ {ABE} \right]}} = \frac{{4 \times 2\operatorname{tg} x}}{2} = 4\operatorname{tg} x {A_{\vartriangle \left[ {ABE} \right]}} = \frac{{4 \times 2\operatorname{tg} x}}{2} = 4\operatorname{tg} x](/images/jlatex/64083a7e548b196d88c249dfa6f9a4c3.gif)
![{A_{\square \left[ {ABCD} \right]}} = {4^2} = 16 {A_{\square \left[ {ABCD} \right]}} = {4^2} = 16](/images/jlatex/683c9506c3d076a552ec4721f2d03522.gif)

2.
A função  é contínua em
é contínua em ![\left] {0,\frac{\pi }{4}} \right[ \left] {0,\frac{\pi }{4}} \right[](/images/jlatex/1843b8ee4ace095a52ff515e842c869e.gif) , pelo que também é contínua em
, pelo que também é contínua em ![\left[ {\frac{\pi }{{12}},\frac{\pi }{5}} \right] \left[ {\frac{\pi }{{12}},\frac{\pi }{5}} \right]](/images/jlatex/c4340eabf9a2494edf35196f587362a3.gif) .
.


Como  , então pelo Teorema de Bolzano, existe pelo menos um
, então pelo Teorema de Bolzano, existe pelo menos um ![x \in \left] {\frac{\pi }{{12}},\frac{\pi }{5}} \right[ x \in \left] {\frac{\pi }{{12}},\frac{\pi }{5}} \right[](/images/jlatex/08862529599f51930f124d1e41b5d4fe.gif) , tal que
, tal que  .
.
![\left[ {ABE} \right] \left[ {ABE} \right]](/images/jlatex/5ed4c69f7b62a9b923db1773cb12c6d7.gif) ,
, ![\left[ {BCF} \right] \left[ {BCF} \right]](/images/jlatex/f068e07053c05b6ed15028b9c167dce8.gif) ,
, ![\left[ {CDG} \right] \left[ {CDG} \right]](/images/jlatex/fe95f8a2de609f2b806a7696a89b24a3.gif) e
e ![\left[ {DAH} \right] \left[ {DAH} \right]](/images/jlatex/efe553cd8542b2725f02b7e41c5cb027.gif) são geometricamente iguais.
são geometricamente iguais.![\left[ {AB} \right] \left[ {AB} \right]](/images/jlatex/103109231bf469cee07093a66be902fa.gif) .
.
![{A_{\vartriangle \left[ {ABE} \right]}} = \frac{{4 \times 2\operatorname{tg} x}}{2} = 4\operatorname{tg} x {A_{\vartriangle \left[ {ABE} \right]}} = \frac{{4 \times 2\operatorname{tg} x}}{2} = 4\operatorname{tg} x](/images/jlatex/64083a7e548b196d88c249dfa6f9a4c3.gif)
![{A_{\square \left[ {ABCD} \right]}} = {4^2} = 16 {A_{\square \left[ {ABCD} \right]}} = {4^2} = 16](/images/jlatex/683c9506c3d076a552ec4721f2d03522.gif)

 é contínua em
é contínua em ![\left] {0,\frac{\pi }{4}} \right[ \left] {0,\frac{\pi }{4}} \right[](/images/jlatex/1843b8ee4ace095a52ff515e842c869e.gif) , pelo que também é contínua em
, pelo que também é contínua em ![\left[ {\frac{\pi }{{12}},\frac{\pi }{5}} \right] \left[ {\frac{\pi }{{12}},\frac{\pi }{5}} \right]](/images/jlatex/c4340eabf9a2494edf35196f587362a3.gif) .
.

 , então pelo Teorema de Bolzano, existe pelo menos um
, então pelo Teorema de Bolzano, existe pelo menos um ![x \in \left] {\frac{\pi }{{12}},\frac{\pi }{5}} \right[ x \in \left] {\frac{\pi }{{12}},\frac{\pi }{5}} \right[](/images/jlatex/08862529599f51930f124d1e41b5d4fe.gif) , tal que
, tal que  .
.
![\left[ {ABCD} \right] \left[ {ABCD} \right]](/images/jlatex/7c39be72ce8fa6c0bf88b67de000cf8a.gif) .
.

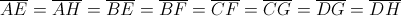
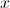 é a amplitude, em radianos, do ângulo
é a amplitude, em radianos, do ângulo 
![x \in \left] {0,\frac{\pi }{4}} \right[ x \in \left] {0,\frac{\pi }{4}} \right[](/images/jlatex/1727a76c7b24d07cc2f02c138d383154.gif)
 .
. e
e  para o qual a área da região sombreada é 5.
para o qual a área da região sombreada é 5.



