Resolução do exercício de matemática:
1.




2.



Como ![\alpha \in \left] {\frac{\pi }{4},\frac{\pi }{2}} \right[ \alpha \in \left] {\frac{\pi }{4},\frac{\pi }{2}} \right[](/images/jlatex/79c2c61dee247ddadb8f507db2bec46e.gif) , tem-se que:
, tem-se que:
Como  e
e  , tem-se que
, tem-se que  .
.
Seja 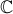 o conjunto dos números complexos.
o conjunto dos números complexos.
1. Seja 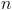 um número natural.
um número natural.
Determine 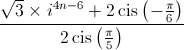 , sem recorrer à calculadora.
, sem recorrer à calculadora.
Apresente o resultado na forma trigonométrica.
2. Seja ![\alpha \in \left] {\frac{\pi }{4},\frac{\pi }{2}} \right[ \alpha \in \left] {\frac{\pi }{4},\frac{\pi }{2}} \right[](/images/jlatex/79c2c61dee247ddadb8f507db2bec46e.gif) .
.
Sejam 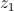 e
e 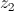 dois números complexos tais que
dois números complexos tais que 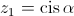 e
e 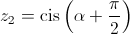 .
.
Mostre, analiticamente, que a imagem geométrica de 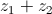 , no plano complexo, pertence ao 2.º quadrante.
, no plano complexo, pertence ao 2.º quadrante.
Resolução do exercício de matemática:
1.




2.



Como ![\alpha \in \left] {\frac{\pi }{4},\frac{\pi }{2}} \right[ \alpha \in \left] {\frac{\pi }{4},\frac{\pi }{2}} \right[](/images/jlatex/79c2c61dee247ddadb8f507db2bec46e.gif) , tem-se que:
, tem-se que:


Como  e
e  , tem-se que
, tem-se que  .
.